Elektronikawzad23

w Ciątyńrfd - ELEKTRONIKA W ZADANIACH

Cztii 1: Obliczanie punktów płacy przyrządów półprzewodnikowych

przyjąć że prąd bramki nie płynie, nie występuje zatem spadek napięcia na zastępczej rezystancji 1,5 MH i potencjał bramki jest równy U_G=Ez= 6V. Dla obwodu bramka-źródło możemy napisać:

Uc=Ucs+hRs    (1.12.1)

Wobec tego, żcls = b mamy: b ■ Rs = Uc- U es

czyli:    b = U_G /Rs - Ucs /Rs    (1.12.2)

•o \ /
l"A) \ /
A\ 7
-1 1 i—^	—*—►

Rys. 1.12.4

Ostatnie równanie w układzie współrzędnych b=f (Ugs) ma postać prostej przechodzącej przez punkty (!2mA;0V) i (0 mA; 6 V), czyli wychodzącej z punktu odpowiadającego na osi napięć Ucs wartości Uc -6V    i posiadającej nachylenie

odpowiadające rezystorowi Rs= 0,5 kI2 (patrz rysunek 1.12.4). Prosta ta przecina charakterystykę przejściową tranzystora w punkcie o współrzędnych b = 2 mA i Ucs = 5 V stanowiącym rozwiązanie tego obwodu.

Potencjał    źródła tranzystora wynosi

U_s= Is • Rs= 2 mA • 0,5 kQ = 1 V.

Dla obwodu wyjściowego możemy napisać:

Enn = Id ■ Rd + Uds + h⁴ Rs czyli napięcie dren-źródło wynosi:

Uds = Edd - 1d(Rd + Rs) = 12 V - 2 mA (2 kQ + 0,5 kft) = 7 V, a potencjał drenu U_d = I_sRs + U_ds= 1 V + 7V = 8V

Ad 2. Na charakterystyce przejściowej podano, że obowiązuje ona dla Uds = 2 -r 20 V, co oznacza że charakterystyki wyjściowe b = f (Uds) w podanym zakresie napięć biegną poziomo (prąd b nie zależy w tym zakresie od napięcia dren-źródło Uds)- Oznacza to, że minimalna wartość Uds, którą można przyjąć bez niebezpieczeństwa pojawienia się zniekształceń to 2 V. Czyli Ud mm = Us+ Uds min- I V + 2 V = 3 V, a maksymalny spadek napięcia na rezystorze Rd wynosi b- Romai = 9 V. Tdk więc maksymalna wartość rezystancji w obwodzie drenu to Rpma, = 9 V / 2 mA = 4,5 kft. Wartość minimalna tej rezystancji to Rp_mm = 0, gdyż wtedy Uds = 11 V i tranzystor pracuje także w zakresie pentodowym charakterystyk. Tak więc ostatecznie:

0<Rp< 4.5 kil

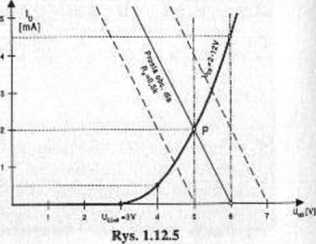
Ad 3. Podłączenie sygnału e„v zmiennego w czasie (np. sinusoidalnego) powoduje, że poprzez kondensator C_w naładowany do napięcia stałego 6 V sygnał ten zostaje podany na bramkę tranzystora. Potencjał bramki zmienia się teraz w czasie zgodnie z zależnością Uc(t) = 6 V + e_wt. W układzie bez kondensatora Cs prosta obciążenia przesuwałaby się w takt zmian sygnału e** równolegle, jak to na rysunku 1.12.5 zaznaczono liniami przerywanymi dla amplitudy sygnału równej I V (czyli zmiany potencjału bazy od 5 V do 7 V), co powodowałoby odchylenia prądu Is w górę i w dół od wartości 2 mA. Dla małych amplitud sygnału e_m możemy założyć, że charakterystyka przejściowa tranzystora jest w otoczeniu punktu P liniowa i wtedy w obecności sygnału wartość średnia prądu nie ulegałaby zmianie.

Zmieniający się w czasie prąd nałożony na prąd stały o wartości równej 2 mA płynie jednak w naszym układzie przez równoległy obwód złożony z rezystora Rs i kondensatora Cs. Przez połowę okresu (gdy prąd źródła Is wzrasta ponad wartość 2 mA) kondensator Cs jest doładowywany, a przez, drugą połowę (gdy prąd źródła 1$ maleje poniżej wartości 2 mA) kondensator Cs jest rozładowywany. Zachowanie układu zależy od wartości pojemności kondensatora Cs (czyli od stałej czasowej rs = Rs • Cs), oraz od szybkości zmian (częstotliwości) sygnału c*_t. Jeśli stała czasowa x$ jest znacznie większa od okresu zmian sygnału (przykładowo dla częstotliwości sygnału 1 kHz okres wynosi 1 ms, czyli pojemność Cs musiałaby być kilkakrotnie większa niż I ms / 0,5 kft = 2 pF) to przez pół okresu napięcie na kondensatorze zmieni się tak nieznacznie, że możemy je uznać za stałe. Omawiane równoległe połączenie rezystora R_s = 0,5 kii z kondensatorem Cs o bardzo dużej pojemności przy wysterowaniu wzmacniacza napięciem przemiennym zachowuje się jak stała SEM o wartości U$ = 1 V. Dla składowej zmiennej mamy w obwodzie źródła impcdancję równą zeru. czyli prosta obciążenia dla tej składowej na rysunku 1.12.5 powinna przebiegać pionowo, a napięcie sterujące obwód bramka-źródło wynosi:

Ucs(t) = U di) - U_s = 6 V +    - 1 V = 5 V + t_m

Pionowemu przebiegowi prostych obciążenia przy wysterowaniu takim samym napięciem odpowiadają większe przyrosty prądu źródła h niż w sytuacji bez kondensatora Cs (co pokazano na rysunku 1.12.5 dla amplitudy równej 1 V). Możemy stwierdzić, że zastosowanie kondensatora Cs prowadzi do wzrostu wzmocnienia dla e^. poprzez eliminację ujemnego sprzężenia zwrotnego na rezystorze Rs.

Natomiast prąd drenu zmieniający się sinusoidalnie wokół wartości /o=2mA wytwarza na rezystancji Rd zmienne napięcie wyjściowe. Sygnał wyjściowy nie jest zniekształcony (odtwarza kształt sygnału wejściowego e„_r jeśli tranzystor dla wszystkich wartości chwilowych napięcia wejściowego pozostaje w obszarze pentodowym (stanowi sterowane napięciem bramki źródło prądowe). Odpowiada to wymaganiu, aby potencjał drenu w chwili odpowiadającej maksymalnej wartości dodatniej sygnału nie spadał poniżej Uomm- U_s + Uosmn- I V + 2 V = 3 V. Z drugiej strony maksymalna wartość chwilowa potencjału drenu (odpowiadająca chwilowemu spadkowi prądu Id do zera) jest równa napięciu zasilającemu 12 V. Zakres zmienności potencjału drenu 12V-3V = 9V odpowiada podwójnej amplitudzie sygnału wyjściowego. Jej osiągnięcie jest możliwe, gdy przyjmiemy spoczynkowy punkt pracy w środku zakresu zmienności, czyli gdy wybierzemy wartość potencjału drenu w punkcie pracy (przy braku sygnału zmiennego) równą Ud- 7,5 V. Odpowiada to spadkowi napięcia w wyniku przepływu prądu spoczynkowego 2 mA równemu /t> •/?/),**» = 4,5 V, a więc odpowiada przyjęciu wartości rezystancji Rodopt = 4,5 V / 2 mA = 2,25 kfl

Kondensator wyjściowy C_wy pozwala na oddzielenie składowej stałej występującej w spoczynkowym punkcie pracy Ud- 7.5 V, a więc na rezystancji obciążenia Rt. podłączonej za kondensatorem mamy już tylko wzmocnione napięcie wejściowe, o zerowej składowej stałej i amplitudzie do 4,5 V. Podobnie jak w innych zadaniach tej części zbioru nie mówimy jakie jest wzmocnienie wzmacniacza, a zatem jakiej odpowiada to amplitudzie napięcia wejściowego.