Elektronikawzad33

w. Oątyfató ELEKTRONIKA W ZADANIACH

Oęić I: Oblkwnie punktów płacy przyrządów półpnKwodniktmyih

skąd obliczamy odpowiadającą temu stanowi wartość napięcia wejściowego:

Uwe = - 0,1 (10 - 5,556) V = - 0.444 V    (1.17.5)

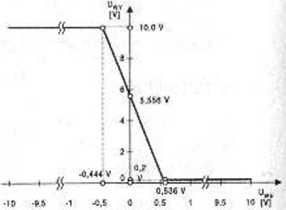
Ad 2. Przebieg charakterystyki U wy - f (Uwe) wyrażający się w zakresie aktywnej pracy tranzystora zależnością (1.17.1) oraz wartości graniczne pokazano na rysunku 1.17.4.

Rozwiązanie 2

Ad 1. W stanie nasycenia prąd kolektora tranzystora wynosi:

r    ~Ucr, 10 V—0,2 V

• r ~    I    — TT~1-—

ikn

9.8 mA

(1.17.6)

\'a granicy stanu nasycenia możemy jeszcze wykorzystać zależność lc= P Ib obliczyć:

Ib = 9,8 mA / 100 = 98 \iA Z rysunku 1.17.2 widać, że skoro U be = 0.6 V to prąd płynąfcy przez rezystor /?/ ze źródła zasilania wynosi h = (10 V- 0,6 V) / 90 k£1 = 104,4 \iA, a więc na granicy stanu nasycenia przez rezystor R₂ płynie prąd:

h = /; - h - 104,4 nA - 98 \iA = 6,4 pA, który na rezystancji R₂ = 10 kśż wytwarza spadek napięcia 64 mV. Tak więc napięcie wejściowe odpowiadające granicy stanu nasycenia musi być

równe:    Rys. 1.17.4

Uw = 600 mV - 64 mV = 536 mV

Dla Uwe = 0 wobec tego, że U be = 0,6 V przez rezystor R1 płynie nadal prąd 1/ = 104,4 mA, podczas gdy ze zwartego do masy wejścia wypływa prąd h = U be / R2 = 600 mV /10 kH = 60pA. Prąd bazy tranzystora ma więc wartość:

^ = /; - /₂ = 44,4 pA, prąd kolektora:    lr -fi -h- 4,44 mA.

a napięcie wyjściowe:    U_m = U_yjs — l_c • R_c -10 V — 4,44 mA • 1 k£2=5,56 V.

Na granicy stanu odcięcia przy napięciu Ube ciągle równym 0,6 V (a zatem przy prądzie l, nadal równym 104,4 pA) prąd bazy staje się równy zeru, czyli cały prąd h płynie przez R₂ = 10 kii wywołując na nim spadek napięcia równy 1,044 V. Tak więc napięcie wejściowe odpowiadające granicy stanu odcięcia musi wynosić:

Uwe = 600 mV - 1044 mV = - 444 mV

Wszystkie przedstawione na rysunku 1.17.4 punkty charakterystyczne wyznaczone w rozwiązaniu 1 pokrywają się z obliczonymi powyżej wartościami.

Zadanie 1.18

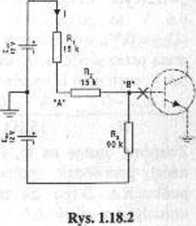
Rys. 1.18.1

Dla układu pokazanego na rysunku 1.18.1

należy:

1.    obliczyć napięcie wyjściowe Uwr przy „wiszącym w powietrzu” (nic podłączonym) wejściu;

2.    obliczyć napięcie wyjściowe Uwr przy wejściu podłączonym do masy (dla Uwe = 0);

3.    wyznaczyć zakres wartości napięcia wejściowego Uwf., w którym tranzystor T pracuje w stanic aktywnym;

4.    dla napięć wejściowych w zakresie 0 < Uwe ^ 12 V wykreślić charakterystykę

przejściową U wy = f ( UwfJ oraz charakterystykę wejściową    = U Uwe)',

Zakładamy, że:

-    przewodzącą diodę wejściową D można zastąpić spadkiem napięcia U_D = 0,6 V niezależnym od wartości prądu diody;

-    prąd wsteczny diody D jest bardzo mały i może być pominięty;

w stanie nasycenia tranzystora napięcie Uce wynosi Uce, = 0,2 V i nie zależy od wartości prądu /<■■;

-    złącze baza-emiter tranzystora T znajdującego się w stanic aktywnym można zastąpić spadkiem napięcia U be = 0,6 V niezależnym od wartości prądu bazy;

-    prądy zerowy i cm tranzystora jest bardzo mały, możliwy do pominięcia;

-    współczynnik wzmocnienia prądowego tranzystora P = 50.

Rozwiązanie

Ad ł. Analizę obwodu rozpoczynamy od sytuacji, gdy do diody wejściowej nie jest podłączone napięcie Uwe, tzn. gdy dioda D „wisi w powietrzu”. Aby zorientować się w jakim stanie znajduje się tranzystor obliczmy potencjał w punkcie B w przypadku, gdyby baza tranzystora nie była do niego podłączona. W tej sytuacji przez dzielnik rezystancyjny R/, R₂, Ri płynąłby prąd:

y Ecc + Em 12 V +12 V Ri+R. + R, 120 kfi a potencjał punktu B wyniósłby :

= 0,2 mA

U_B = Ecc -1 (R, + R₂) = 12 V - 0.2 mA • 30 kfl = 6 V

Ponieważ jest on wyższy od 0.6 V mamy pewność, że podłączenie do tego punktu bazy tranzystora spowoduje przepływ prądu bazy Ib i możemy do dalszych rozważań przyjąć, że potencjał tego punktu odpowiada przewodzącemu złączu i wynosi U_B = U_Be = 0,6 V.

Wyodrębniamy obwód polaryzacji bazy (patrz rysunek 1.18.3) i obliczamy potencjał w punkcie A dla przypadku przewodzącego tranzystora. W tej sytuacji przez dzielnik rezystancyjny R_lr R₂, R₃ płyną prądy: