Elektronikawzad38

w. Ciąźyński - ELEKTRONIKA W ZADANIACH

CięU I: Obliczanie punki ńw procy piZiTłtylów półprzewodnikowych

Zadanie 1.20

Dla pokazanego na rysunku układu

dwustopniowego napięciowego

wzmacniacza prądu zmiennego

należ)':

l. obliczyć punkty pracy tranzystorów Tl i T2 określone przez wartości Ic i Uct,

2. obliczyć maksymalną amplitudę niezniekształconego sygnału wyjściowego;

3. obliczyć wartość rezystancji Rgi, która mogłaby zostać włączona w miejsce źródła prądowego

1

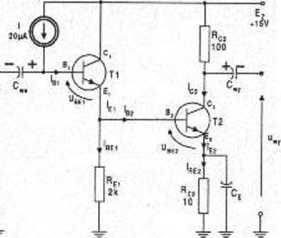
Rys. 1.20.1

/ = 20 pA, bez zmiany punktów pracy tranzystorów.

Zakładamy, żc:

-    złącze baza-emiter przewodzącego tranzystora (Tl i T2) można zastąpić spadkiem napięcia Ube = 0,6 V niezależnym od wartości prądu bazy;

-    prądy zerowe Iceo tranzystorów Tl i T2 są bardzo małe, możliwe do pominięcia;

-    współczynniki wzmocnienia prądowego tranzystorów Tl i T2 wynoszą odpowiednio p\ = 100 i $ = 50;

-    w stanie nasycenia tranzystora T2 napięcie Uce tego tranzystora wynosi Uce, = 0,6 V i nie zależy od wartości prądu Ic;

-    wartości pojemności C_Ht, Ce i C_wy są na tyle duże, że dla częstotliwości wzmacnianego sygnału można przyjąć, żc ich impedancje są równe zeru (kondensatory stanowią zwarcie).

Rozwiązanie

Ad 1. Zakładamy, że obydwa tranzystory znajdują się w stanic aktywnym. Ponieważ

znamy prąd polaryzacji bazy I_Bi = I możemy obliczyć prąd emitera tranzystora Tl:

I_€{ = (fi, +1 )I_B, = (100+1) • 20 pA = 2.02 mA

(1.20.1)

Potencjału Uei nie możemy obliczyć wprost, ponieważ prąd 4/ ma dwie składowe zależne od Uei'.

~ IrE\ + 1K2

Pierwszą z tych składowych obliczamy w zależności od Uei łatwo jako:

(1.20.2)

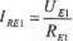
(1.20.3)

Szansę obliczenia drugiej składowej daje nam spostrzeżenie, że:

U_E2=U,_t-U_De: A więc:

(1.20.4)

(1.20.5)

a poszukiwana druga składowa prądu l_Ei> czyli prąd bazy tranzystora T2:

; _ J« _ Uą-Uu* *² ft-fl (P₂ + !)■/?,

£>

Podstawiając zależności (1.20.1), (1.20.3) wyrażenie:

(1.20.6)

(1.20.6) do (1.20.2) uzyskujemy

. u_E\ U_BE2

^F.\ (Pi

z którego możemy już wyznaczyć potencjał Uu, a następnie £7^:

(7.20.7)

(A+1H + -—2,02mA+-^600mV

U„=-

(Ą + 0*g2

51•10 Ś2

= 1,3 V

0,5 mS+

(7.20.5)

5110

^£1 (Pz ⁺ H ^F.2 U_r2 = 1,3 V - 0.6 V = 0,7 V

Teraz z równania (1.20.6) można wyliczyć wartość Jbz-U,_K2 1,3 V-0,6 V

/ =^v"

¹ Bi

(A + 0*_£

51-100

= 1,37 mA

(1.20.9)

a następnie prąd kolektora i napięcie kolektor-emiter tranzystora T2:

/ca-A

Ujm = 68 mA • 100 f2 = 6,8 V U_CE1 = E_cc -U_M-£/„ = 15 V-6,8 V -0,7 V = 7,5 V Tranzystor Tl pracuje więc w punkcie pracy (2mA; 13,7 V) a tranzystor T2 w punkcie (68 mA; 7,5 V). Obydwa tranzystory znajdują się w stanic aktywnym, czyli użycie powyżej zależności dla tego stanu tranzystora było usprawiedliwione i uzyskane wyniki są poprawne.

Ad 2, Przyłożenie poprzez kondensator sprzęgający C_w, napięcia wejściowego powoduje, że prąd bazy tranzystora Tl oscyluje wokół stałej wartości 20 pA, co z kolei wymusza odpowiednie zmiany prądów /c i h obydwu tranzystorów wokół ich wartości spoczynkowych w punktach pracy. Zastosowanie kondensatora Ce o dużej pojemności włączonego równolegle do rezystancji Ke2 powoduje, żc pomimo zmian prądu 1_E2 potencjał emitera Uaz pozostaje stały (opisano ten mechanizm dokładniej w zadaniu 1.12). Aby określić największą osiągalną amplitudę niezniekształconego napięcia wyjściowego wystarczy zatem prześledzenie zakresu zmian potencjału kolektora, przy których tranzystor T2 pozostaje w sumie aktywnym.

Spoczynkowy potencjał kolektora tranzystora T2 wynosi:

U_C2=U_E2+ U cez = (0,7 + 7.5) V = 8,2 V,

a więc przy ujemnych wartościach chwilowych przemiennego sygnału wejściowego odpowiadających zmniejszeniu prądu Ic2 do zera, potencjał kolektora może wzrosnąć do wartości Ecc= 15 V, czyli o 6,8 V. Wynika z tego, że dodatnia amplituda zmiennego napięcia wyjściowego (za kondensatorem sprzęgającym C_H?). przy której nie wystąpiąjeszcze zniekształcenia może wynosić 6,8 V.

Przy dodatnich wartościach chwilowych przemiennego sygnału wejściowego odpowiadających wzrostowi prądu Icz potencjał kolektora spada i jeśli wzrost 7cz jest wystarczająco duży tranzystor może wejść w stan nasycenia. Odpowiadałoby to obniżeniu się potencjału kolektora do wartości:

U_a = V_F.2 + (/c& = 0,7 V + 0,6 V = 1,3 V