fotazksiki2

Rys. 8.6

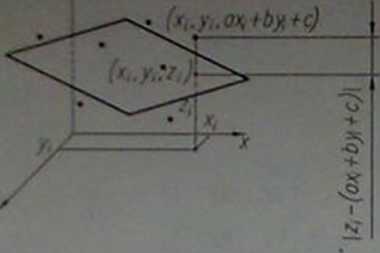
Płaszczyzna średnia wyznaczona z warunku najmniejszej sumy kwadratów

Wartości parametrów a, b_% c równania płaszczyzny wyznacza się Ao rozwiązanie następującego układu równań (liniowych):

^x‘ ^+hi (^x*y> ) + ‘X ^x> =Ż    )

^/=1    /=1    i=l    i=l

^ai (^x<y.)+^v> ^{+ C}Ż y> =Ż (y*)

i=i i=i n

1=1    /=!    i=l

n    n    _n

^x<^{+ b}lL^v'⁺ cn =X^r'

i=i    i=i    i=i

Rozw iązanie układu jest następujące:

-Ł; _b=wt, _{C =} 5Ł

W w w

gdzie:

Wk =

Z*? IMI*.		Z(^j<^z/) Z (*<>’.) Z ^z-
Z O/*) Zk I.v,	\Wa =	Z0'/^z<) Z yf Z y>
Z^1' Z* «		Z Z ^ "
Z ^rr Z(*«^z«) Z*/		Z ^v-^2 Z(-v'/) Z(*-^z.)
ZOw) Z(r.^z.) 2>,	;fvc =	Z(*<zł) Z.v,^2 Z(*^z0
Z*< Z^z« n		Z*« Z^ Z^z/

(dyskietka. ASS).

8.11. Płaszczyzna przylegająca

Kombinatoryczny algorytm wyznaczania płaszczyzny przylegającej

do powierzchni zdefiniowanej przez zbiór punktów (x_lty_h z,), gdzie / = 1.

//, a // — liczba punktów', jest analogiczny do algorytmu wyznaczania prostej przylegającej. Spośród płaszczyzn wyznaczonych przez każdą niewspó I liniową trójkę punktów należy wybrać tę, która spełnia

następujące warunki:

• wszystkie pozostałe punkty powierzchni leżą po jednej stronie

płaszczyzny',

•    odległość najbardziej oddalonego punktu od tej płaszczyzny jest

najmniejsza.

Jeśli znaleziona płaszczyzna leży na zewnątrz materiału, to jest to płaszczyzna przylegająca; w przeciwnym razie płaszczyznę przy legającą otrzymuje się przez równoległe przesunięcie otrzymanej płaszczyzny do najbardziej oddalonego punktu powierzchni. Warunkiem pozwalającym na stwierdzenie, po której stronie płaszczyzny leży' punkt, jest znak wyrażenia zj -ax\ - by\ -c (patrz: rozdz. 8.16), gdzie: (x\, y_if zj) — współrzędne punktu, a, b, c — parametry' równania płaszczyzny w postaci kierunkowej (rozdz. 8.9). Program komputerowy napisany w Turbo Pascalu, realizujący ten algorytm, zamieszczono na dy skietce (dyskietka, ASP).

8.12. Odległość punktu od prostej na płaszczyźnie

Odległość punktu od prostej danej równaniem:

y = ax + b

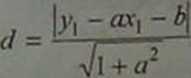
oblicza się wg wzoru ¹

gdzie (x\,y\) — współrzędne punktu. Jeśli y_} - ax_} - b > 0, to pun y, - ax_} - b < 0, to punkt leży- pod p

1

I - uuiiniu-

-ax_l-b> 0, to punkt leży nad prosUL a b < 0. to punkt leży pod prostą (dyskietka. ADO)