Rzuty mongea138

81

stopadłe) i znaleźć ich odpowiedniki na płaszczyźnie q>. Średnicami okręgu na rys. 76 są odcinki A-B i C-D, a ich odpowiednikami w elipsie są jej średnice sprzężone I-II i lll-IV. Punkty I, II, III, IV są końcami średnic sprzężonych elipsy przekroju. Rzutem pionowym elipsy jest elipsa o średnicach l"-H" i IH"-IV".

Ponieważ płaszczyzna cp przecina wszystkie tworzące powierzchni, a więc także jej tworzące konturowe, więc na każdej z nich znajduje się jeden punkt elipsy. Jeden punkt elipsy leżący na tworzącej konturowej może być tylko punktem styczności krzywej do tej tworzącej. Na rys. 76 są to punkty P i Q. Skonstruowano je jako punkty przebicia płaszczyzny (p przez tworzące przechodzące przez punkty 1 i 2.

Uwaga: Gdyby z jakichś powodów płaszczyzna tnąca nie mogła być prostopadła do jednej z podstawowych rzutni (tak jak <p do tti), to korzystając z transformacji, można płaszczyznę tnącą wraz z walcem tak „ustawić", by była prostopadła np. do tu. Zadanie rozwiązuje się wówczas na 7D tak, jak je rozwiązano na 7ti na rys. 76.

Przekrój powierzchni walcowej obrotowej konstruuje się podobnie jak powierzchni nieobrotowej. Przekrój taki odwzorowano na rys. 79, na którym również zilustrowano rozwinięcie powierzchni walcowej obrotowej.

9.2. Rozwinięcie powierzchni walcowej nieobrotowej

W konstrukcji rozwinięcia powierzchni walcowej korzysta się z omówionej wcześniej konstrukcji rozwinięcia graniastosłupa. Zakłada się, że rozwijana powierzchnia walcowa opisuje pewien pomocniczy graniastosłup, którego krawędziami bocznymi są tworzące opisującej go powierzchni (rys. 77). Podstawą graniastosłupa jest więc wielokąt wpisany w okrąg kierujący powierzchni.

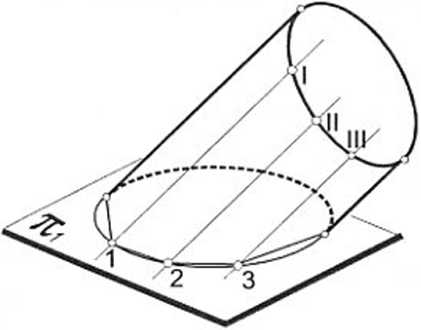
Rozwinięcie pobocznicy pomocniczego graniastosłupa pośredniczy w rozwinięciu opisanej na nim powierzchni i jest jego przybliżeniem. Rozwinięcie graniastosłupa nie może być uznane za tożsame z rozwinięciem powierzchni, ale dla celów praktyki inżynierskiej takie przybliżenie wystarcza (komentarz na ten temat - dalej), zwłaszcza jeżeli wpisany graniastosłup wyposaży się w dostatecznie dużą liczbę ścian bocznych. Rozwinięcie jest tym dokładniejsze, im mniejsze są Rys. 77    odległości między tworzącymi walca -

krawędziami graniastosłupa (byłoby ści słe, gdyby te odległości były zerowe).

Za podstawę pomocniczego graniastosłupa przyjmuje się wielokąt foremny, wpisany w okrąg kierujący powierzchni. Z dokładnością dostateczną dla celów dydaktyki wystarczy wpisanie w okrąg kierujący foremnego dwunastoką-ta. Korzystanie z wielokątów foremnych upraszcza i przyspiesza konstrukcję rozwinięcia.