geometria anlityczna 2 podstawa

46.

Punku- A = 11.-2). C = {4.2) są dwoma wierzchołkami trójkąta równobocznego ABC'. Wysokość tego trójkąta jest równa _

w 3 B. —	C.	5v3	D. M
3		6	9

A.

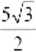
19.

Ile punktów wspólnych ma prosta o równaniu j = -,v - 2 z okręgiem o środku w początku układu współrzędnych i promieniu 2?

A. 0    B. 1    C. 2    D. 3

20.

Prosta / ma równanie y = 2.v-l 1. Wskaż równanie prostej równoległej do /.

A.

v = 2x

B.

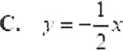
D.

21.

Wskaż równanie okręgu o środku .S' = (.1. - 2) i promieniu ? = 2.

A.	(v-l	;r-i.v-2ł‘ =2
B.	(.V -1	f •+ (v - 2 )^: = 2
C.	(a -1	)^:+(.v-2)^: =4
D.	(a -1	)^:-iy-2)^: =4

22.

Które z równań opisuje prostą prostopadłą do prostej o równaniu y = 4x - 5 ?

A. y = -4.v -r 3    B. y = ~—x - 3    C. y=—x+3 D. v = 4.v-3

4    4

23.

Punku- A = {—1.3) i C = (7.9) są przeciwległymi wierzchołkami prostokąta ABCD. Promień okręgu opisanego na tym prostokącie jest równy

A. 10    B. 6>/2    C. 5    D. 3>/I

Liczba punktów wspólnych okręgu o równaniu (.v + 3 f — (y —1)“ = 4 z osiami układ współrzędnych jest równa

A. 0    B. 1    C. 2    D. 4

26.

Środek S okręgu o równaniu x* + y~ + 4x — 61 — 221 = 0 ma współrzędne

A. S = (-2.3)    B. S = (2.-3) C. 5 = (-4.6) D. 5 = (4.-6)

27.    (6pkt)

Punkty A-(7.3) są kolejnymi wierzchołkami kwadratu ABCD. Wyznacz współrzędne wierzchołkaC tego kwadratu.

28.    (6pkt)

Dwa boki równoległoboku zwierają się w prostych o równaniach AB: y - -y.v - 2, AD:y = 2x - 5. środek symetrii równolegtoboku ma współrzędne ,V = (5,2) Wyznacz współrzędne wierzchołka li tego równoległoboku.

29.    (2pkt)

Wyznacz rów nanie prostej prostopadłej do prostej y --2.t + 8 przechodzącej przez punkt A =(6,- 1)

30.    (4pkt)

Okrąg o równaniu ,v" - 6.v + y * - 2.y +2 = 0 i prosta ,r + J v + 2 = 0 przecinają się w punktach A, li. Wyznacz długość cięciwy Ali tego okręgu.

31.    (2pkt)

Dany jest wierzchołek trójkąta równobocznego C - (- 4,2). Bok Ali zawarty jest w prostej o równaniu 2.v + 4y - 5 = 0. Wyznacz długość boku tego trójkąta.

32.    (2pkt) _ wiś-KŁcboCkt.

Dane są dwa przeciwległo-bok-i kwadratu A =( 1,- 3),C’ = (-5,- 1). Wyznacz obwód tego kwadratu.

33.    (2pkt)

Odcinek Ali jest wysokością trójkąta rów nobocznego. Oblicz długość boku trójkąta, jeśli wiadomo ze A -{~3,-2),B~(5,2 ).

Razem 50 pkt.