Image 130

żadnymi przepisami administracyjnymi. Wymagania współczesnej technologii produkcji samochodów a także kształtowanie się kosztów produkcji sprawiają, że rozpoczęcie produkcji samochodów związane jest z ogromnymi nakładami kapitałowymi. Zgodnie z niektórymi ocenami specjalistów produkcję samochodów opłaca się rozpoczynać wówczas, jeżeli roczna produkcja może osiągnąć przynajmniej 100 000 egzemplarzy. Równocześnie koniunktura na rynku samochodowym nie jest stabilna i nie gwarantuje nieustannego wzrostu popytu na samochody. Wejście nowych producentów na oligopolistyczny rynek samochodowy jest praktycznie niemożliwe, a niektóre, znane od dawna, firmy samochodowe walczą o przetrwanie na tym rynku.

(4) Pełna informacja o rynku.

Podobnie jak w poprzednich modelach rynku także w odniesieniu do oligo-polu przyjmuje się, że podmioty posiadają doskonałą informację o rynku.

DUOPOL

Duopol jest szczególnym przypadkiem oligopolu i przedstawia rynek, na którym działają jedynie dwaj producenci (sprzedawcy) oferujący ten sam produkt. Działania jednego producenta są zależne od działań drugiego producenta. Współzależności między dwoma przedsiębiorstwami mogą dotyczyć procesu wyznaczania wielkości produkcji lub wyznaczania poziomu cen sprzedaży. Mechanizmy funkcjonowania duopolu zależą od przyjętych założeń odnośnie charakteru współzależności między przedsiębiorstwami. Najbardziej znane modele duopolu zostały opracowane przez A. Cournota (publikacja w 1838 r.), F. Y. Edgewortha (1925 r.) oraz E. Chamberlina.

Model Cournota opiera się na założeniu jednorodności produktu oraz przyjęciu, że koszty produkcji obydwu producentów są takie same. Ponadto koszty marginalne (KM) wynoszą zero, czyli pokrywają się z osią odciętych.

Analizę duopolu można rozpocząć od sytuacji, w której na rynku monopolu pełnego pojawia się drugi producent tego samego produktu. Reakcje producentów polegają na ustalaniu wielkości produkcji, przy czym każdy z nich zakłada, że wielkość produkcji konkurenta pozostaje niezmienna. Każdy z duopolistów przyjmuje, iż jego działania nie wywołują reakcji produkcji przedsiębiorstwa konkurencyjnego. Pomimo tego proces kolejnych dopasowań doprowadza duopol do stanu równowagi.

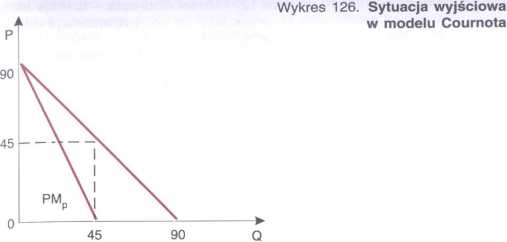
W punkcie wyjściowym, przedstawionym na wykresie 126, dana jest funkcja popytu rynkowego D = 90 - P. Monopol maksymalizuje zysk sprzedając wielkość produkcji Q = 45 po cenie P = 45. Zysk monopolu wynosi 2 025 (Q x P = = 45 x 45 = 2 025).

Przypomnijmy, że w przypadku liniowej funkcji popytu przychód marginalny równa się zero (PM_p = 0) wówczas, gdy wielkość produkcji odpowiada połowie wielkości popytu rynkowego dla ceny równej zero: PM_p = 0 dla 1/2 Q₀ (Q₀ jest wielkością popytu dla P = 0).

Jak zmieni się sytuacja rynkowa w momencie pojawienia się drugiego producenta? Proponując rozwiązanie A. Cournot założył, że każda z firm traktuje wielkość produkcji konkurenta jako daną.

Całkowita produkcja rynkowa jest sumą produkcji firmy 1 i firmy 2:

Q = Q, + Q₂ = 90 - P.

Przyjmijmy, że firma 1 wyznaczyła wielkość produkcji na poziomie Q_r W rezultacie popyt na produkty firmy 2 wynosi:

Q₂ = (90 - Q,) - P

Oznacza to, że firma 2 bierze pod uwagę tę część popytu rynkowego, która pozostała jako różnica między popytem rynkowym i wielkością produkcji wyznaczoną przez firmę 1.

Uwzględniając popyt Q₂ firma 2 wyznacza wielkość produkcji maksymalizującą zysk:

0₂

90 - Q,

2

Firma 2 produkuje i sprzedaje połowę wielkości popytu (przy P = 0), którą pozostawiła firma 1. Wielkość produkcji firmy 2 zależy od zrealizowanej produkcji przez firmę 1. Jeżeli np. firma 1 zdecydowała wyprodukować 60 jednostek, firma 2 będzie wytwarzać: (90 - 60)/2 = 15. Cena rynkowa wynosić będzie w tym przypadku: 90 - (Q, + Q₂) = 90 - (60 + 15) = 15. „

Równocześnie Q₂ = 90 - Q,/2 jest funkcją reakcji firmy 2 na decyzje o wielkości produkcji podejmowane przez firmę 1. W podobny sposób można wyznaczyć funkcję reakcji firmy 1 na decyzje firmy 2. Funkcja ta ma postać: Q, = 90 - QJ2. Funkcje reakcji obydwu firm prezentuje wykres 127A.

261