Image79

156

156

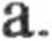
A = {(R, O, R), (R, R, 0), (0, R, R), (R, R, R)},

P(A)

b. Zdarzeniem przeciwnym do opisanego w zadaniu jest

A' = {(0, 0, 0)},

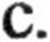
A = {(0,    R,R), ( R,0,    (R, R, 0)},

5.11

a. Wszystkich możliwych zdarzeń jest tyle, ile wszystkich kombinacji 5-ele-mentowych zbioru złożonego z 10 elementów. Zatem ilość wszystkich zdarzeń elementarnych jest równa

Liczba zdarzeń sprzyjających zdarzeniu A jest równa

Zatem

P(A) =

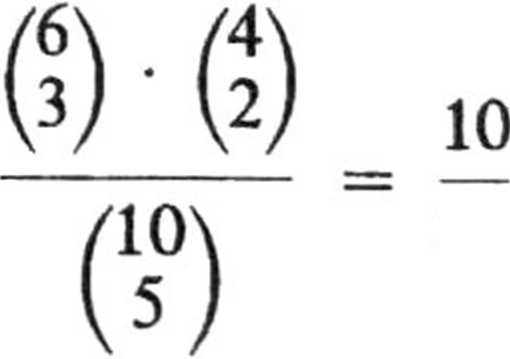
b. Niech A' będzie zdarzeniem przeciwnym do A, tzn. takim, że wszystkie wylosowane kule będą czarne

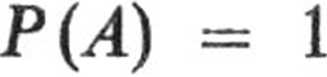
P(A') =

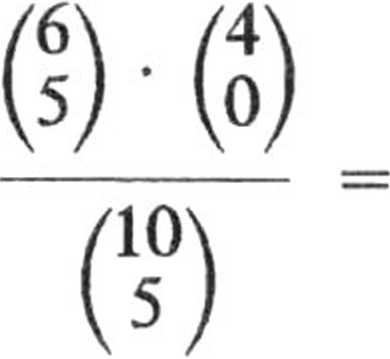
1

42⁹

P(A')

41

42*

c. Zdarzenie przeciwne do A polega na tym, że wylosujemy 5 kul czarnych lub 4 kule czarne i 1 białą.

5.12. Zdarzeniem przeciwnym do A będzie zdarzenie A' takie, że student nie odpowie na 4 pytania lub na 3 pytania bądź na 2 pytania. Zatem

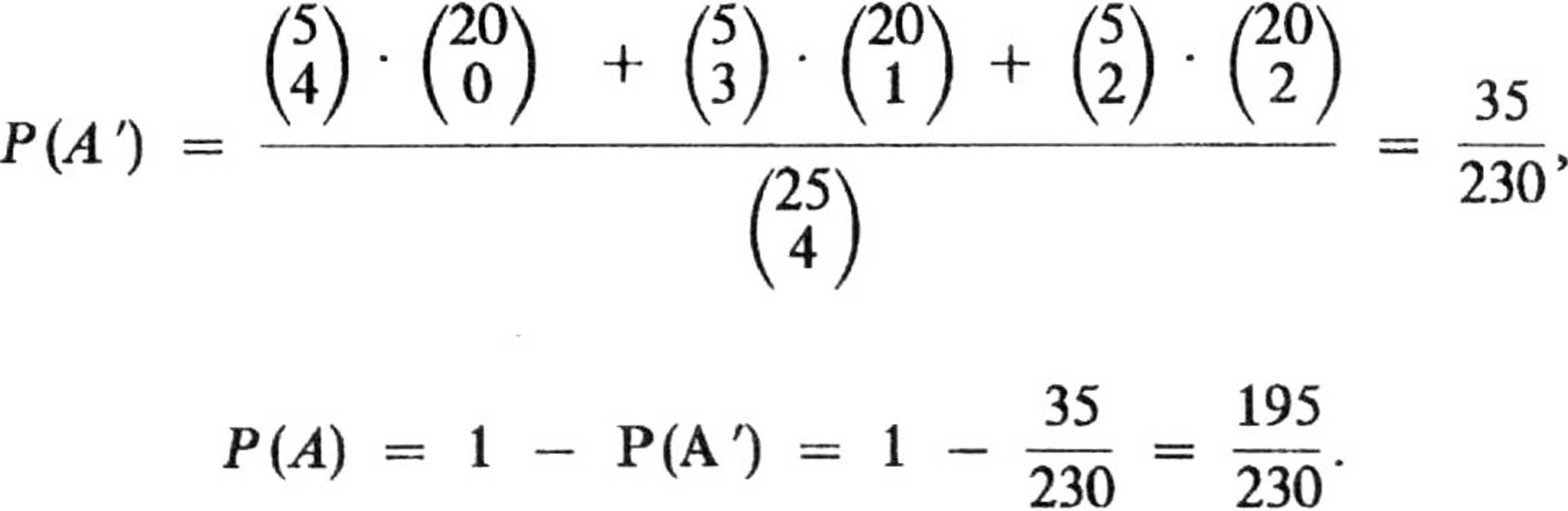
5.13. Niech A₁, A₂ i A₃ oznaczają odpowiednio zdarzenia polegające na tym, że trafił pierwszy, drugi i trzeci z zawodników , a B niech oznacza zdarzenie, że cel został trafiony.

B = A_t u A₂ u ,4₃;

A_it A₂, A₃ są zdarzeniami niezależnymi