Image82

162
X (ln nl + a -f /?£,) dnl = O,
i
gdzie a i p są nieoznaczonymi bliżej czynnikami. Równanie to będzie spełnione, gdy dla każdego wskaźnika i z osobna będzie
ln nt + a + fi Ei = 0.
(a + /?E£)
ty = e
Otrzymane prawo rozkładu Maxwella-Boltzmanna określa liczbę punktów fazowych ni w i-tym elemencie przestrzeni fi w najbardziej, w danych warunkach, prawdopodobnym stanie makro układu złożonego z n cząstek, o sumarycznej energii E.
6.3
a. Liczba cząstek posiadających energię translacji w jednym stopniu swobo dy zawartą między E s. E + dE jest równa
dn"
C n E 2
E
kT
dE,
przy czym spełniony być
usi warunek normalizacji
II
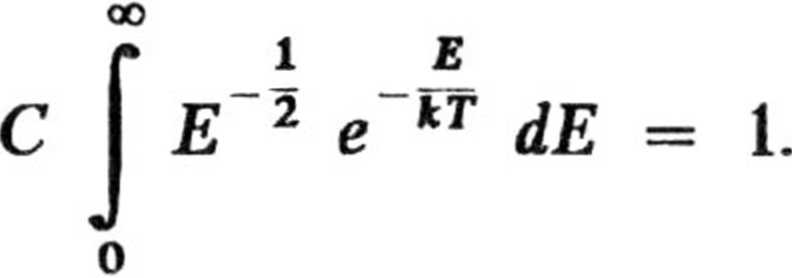
lenną
Wprowadzając nową z
o trzy
II
ujemy
II
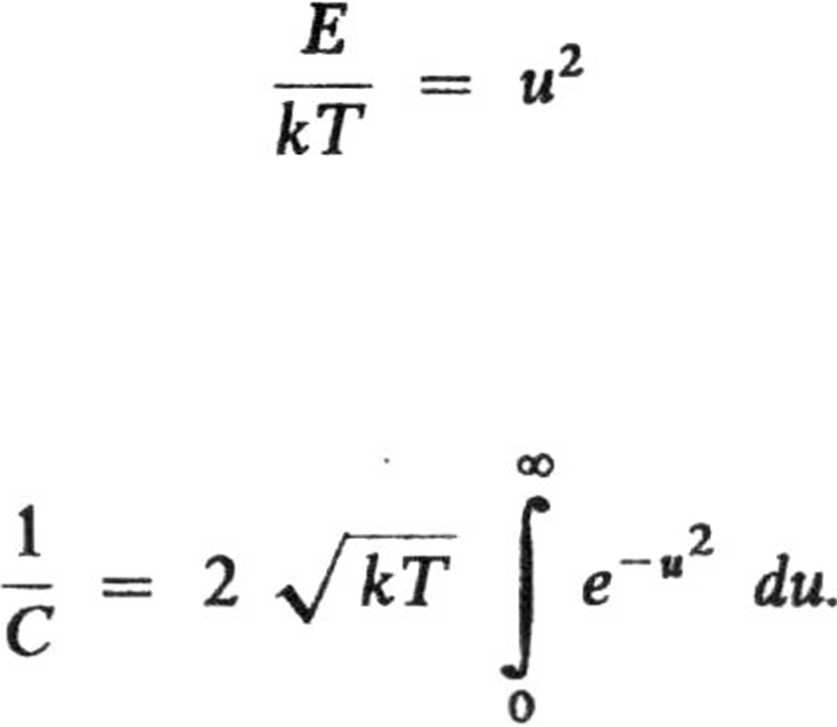
1
C
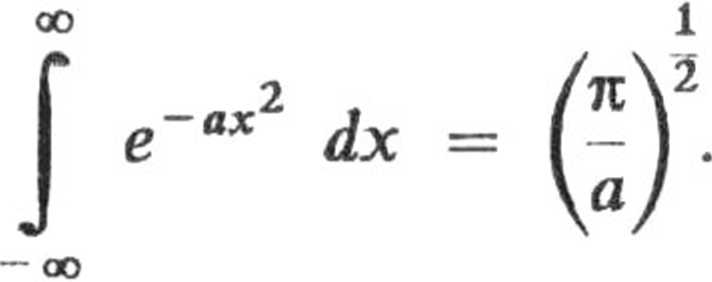
Wobec całki typowej
mamy
(nk T)if2 ’
a równanie Maxwella-Boltzmanna przyjmuje postać
dri' =
n
(nkT)1'2
E
1
2
E
IT
dE.
b. Dla cząstek o dwóch stopniach swobody translacji warunek normalizacji gęstości prawdopodobieństwa, że energia translacji przyjmie wartość z przedziału (E, E + dE) ma postać
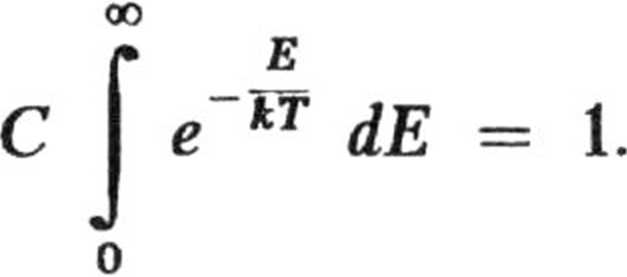
1
kT’
Stąd
C
a liczba cząstek posiadających energię translacji w dwóch stopniach swobody zawartą między E a E + dE jest wyrażona wzorem
n
kT
dn" =
E
kT dE.
c. W tym przypadku warunek do wyznaczenia szukanej stałej normującej przybiera postać
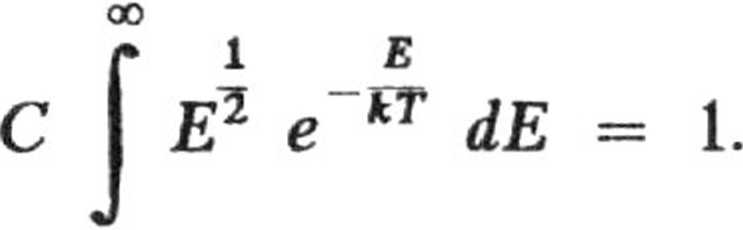
Wyszukiwarka
Podobne podstrony:
Image82 (7) 162X (ln nt + a + pEJ dn, = O, i gdzie a i p są nieoznaczonyn gdy dla każdego wskaźnika
360 V. Funkcje wielu zmiennych gdzie u.x + a.2 + ...+a.„=k jeśli zaś u jest funkcją x, y, ..., z, to
22200 Take the a train L Ł~© 9. Take The “A” Train0 PLAY 6 CHORUSES (. = 162) INTRO (Pmw Cuss l (4x)
77820 PolandPFX21 1Cent 1969 b donated BONY TOWAROWI BAW U POlSKA KASA OW< SA Nł£ POOCC&AM U
28235 str223 § 3. RÓWNANIE LAPLACE’A 223 gdzie A(x, y, z) są punktami obszaru Q (patrz rys. 4.5), B(
skanuj0026 (93) 279 279 gdzie: a i a - są odpowiednio ilością odcinków podstawy czasu T [s] w czasi
więcej podobnych podstron