IMG00063

4. Skręcanie prętów o niekołowych kształtach przekroju poprzecznego

4.5. Skręcanie swobodne prętów o przekrojach otwartych

W przypadku skręcania swobodnego prętów o przekrojach otwartych jednostkowy kąt skręcenia całego pręta jest taki sam, jak jednostkowe kąty skręcenia poszczególnych części przekroju. Jeżeli przekrój poprzeczny pręta składa się z kilku prostokątów, największe naprężenia tnące pozostaną w prostokącie o największej grubości.

W celu uproszczenia obliczeń ograniczymy rozważania do przekrojów złożonych z wąskich prostokątów. Z tablicy 4.1 widać, że dla wąskich prostokątów t]\ = r/2 = 1/3 i wzór (4.7) na maksymalne naprężenia tnące w pręcie o kształcie wąskiego prostokąta wyrazi się w postaci

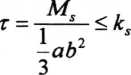
(4.5)

kąt skręcenia zaś

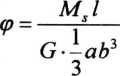
(4.6)

Przez analogię do wzoru (2.27) na kąt skręcenia walu pełnego mianownik we wzorze (4.6) zwany jest sztywnością na skręcanie C, równą iloczynowi modułu sprężystości postaciowej G i sztywności geometrycznej przekroju na skręcanie J_s

(4.7)

C = GJ_S

gdzie dla wąskiego prostokąta •/* = ^aó³.

Wzory (4 5) i (4.6) przybierają więc postać

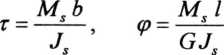
W przypadku pręta o przekroju złożonym z wąskich prostokątów sztywność geometryczna na skręcanie J_s przekroju jest sumą sztywności na skręcanie prostokątów składowych

i=n

1

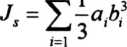
(4.8)

Największe naprężenia tnące w takim pręcie powstaną w środku dłuższych boków prostokąta o największej grubości ó_max spośród wszystkich prostokątów stanowiących przekrój poprzeczny pręta

63