img072

238 V. Metoda reprezentacyjna

powtórnie wylosowany do próby- Gdy populacja generalna ma skończoną liczbę N elementów i stosuje się losowanie zależne próby, to estymatory mają wariancje określone innymi wzorami niż przy losowaniu niezależnym. przy czym wariancje estymatorów w losowaniu zależnym są mniejsze niż w losowaniu niezależnym. Wprawdzie gdy populacja jest bardzo duża, to różnica la nie ma praktycznego znaczenia, ale przy małych populacjach, np. rzędu setek czy mniejszych, zysk na efektywności danego estymatora przy stosowaniu losowania zależnego może być znaczny w stosunku do losowania niezależnego. Gdy szacujemy średnią wartość m w populacji generalnej* zwykły estymator tej średniej, czyli średnia z próby x, ma w przypadku schematu losowania zależnego wariancję określoną wzorem

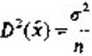
N-n ;Y-f ’

(5-1)

gdzie cń jest wariancją populacji* A^rjest liczebnością populacji, a n liczebnością próby.

W metodzie reprezentacyjnej, gdzie rozważa się populacje skończone, wygodnie jest zamiast wariancji er¹ w populacji, użyć wariancji S² określonej wzorem

(5.2)

S² = ^jV <r²= —

,V-I iV-Uxi

V (X_k-tn)^z.

Wzór na wariancję D*(x) przyjmuje wtedy postać

u

(5-3)

Gdy populacja ma rozkład zbliżony do normalnego (ze względu nąj skończoną liczbę N elementów populacji jej rozkład nie może być dokład-j nie normalny), wtedy można 2budować przedział ufności dla średniej m| w populacji. W poniższych modelach podane będą wzory na przedział] ufności dla średniej m w populacji dla losowania zależnego oraz na trzebną liczebność próby do oszacowania średniej m z żądaną z góry kład nością. Wzory te oparte są na rozkładzie normalnym i rożki t Studenta.

Model I, Populacja generalna ma skończoną liczbę N elementów. Rozkład badanej cecby mierzalnej X w populacji jest zbliżony do normalnego o średniej m i znanej wariancji S². Z populacji tej wylosowano zależnie próbę n elementową, na podstawie której należy¹ oszacować wartość średnią m w populacji.

Przedział ufności dla średniej m wyznacza się ze wzoru

( S ¹ n    5 f" n)

(5.4) P    |l--<m<x^_łT 'h-Ul-a,

(.    _v- n \    jN    v n \ Aj

gdzie Sjest średnią uzyskaną z wyników n elementowej próby, a u_m jest wartością odczytaną z tablicy rozkładu -¥(0, I) dla ustalonego z góry współczynnika ufności 1 —a w taki sposób, by    U<u_a}= \ -a.

Uwaga. Ze wzoru podanego wyżej na przedział ufności można korzystać także, gdy populacja nie ma wprawdzie rozkładu zbliżonego do normalnego, ale próba jest duża.

Model IL Populacja generalna ma skończoną liczbę N elementów. Rozkład badanej cechy X w populacji jest zbliżony do normalnego o średniej z« i nieznanej wariancji S^z. Z populacji tej wylosowano zależnie próbę rt-elementową, z wyników które] obliczono średnią x oraz wariancję

**-A i

n — i i-i

Przedział ufności dla szacowanej średniej m populacji wyznacza się wtedy ze wzoru ^<5-⁵'

gd2ie ś ^-JT², a /„jest wartością odczytaną z tablicy rozkładu t Studenta dla u - ł stopni swobody i dla ustalonego z góry współczynnika ufności 1—a w taki sposób, by P{—/_ł<f<r*}= 1 — a.

Gdy próba jest duża (n> 120), wtedy w modelu tym zamiast wartości t_K używamy jak w modelu I wartości u_a odczytanej z tablicy rozkładu normalnego.