img022 2

»> Wykład z fizyki «<    ROZWIĄZANIE:

Energię kinetyczną każdej lokomotywy możemy wyznaczyć z równania (5.39), ale musimy znać jej prędkość tuż przed zderzeniem oraz jej masę. Przyspieszenie każdej z lokomotyw było stałe, więc do obliczenia jej prędkości v tuż przed zderzeniem możemy zastosować wzory dla ruchu jednostajnie przyspieszonego.

5 =

* = V +

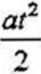
v = v₀*far

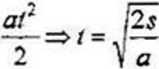
Ponieważ v₀ = 0_r a s = 3,2 • 1 O³ m (jest to połowa początkowej odległości lokomotyw), więc mamy stąd:

\-at

v^: = 250 = 2 -^0,26    • (s,2 • 10³m)

(tzn. v wynosi około 150 km/h).    _r = 40.$—

s

Masę każdej z lokomotyw można wyznaczy ć, dzieląc jej ciężar przez g:

m

9.814

Teraz możemy już obliczyć z równania (5.39) łączną energię kinetyczną obydwu lokomotyw' tuż przed zderzeniem. Otrzymujemy:

^Ą“²{T‘)“^²²'¹°^5fe){^4W7

-2-10V

Przebywanie blisko tego zderzenia było równie bezpieczne, jak przebywanie w pobliżu wybuchającej bomby.    _

>» Wykład z fizyki «<

V---

energii mechanicznej

Energia mechaniczna układu jest sumą jego energii potencjalnej E_p oraz energii kinetycznej E_k wszystkich jego składników:

F 5= F + F ‘-mech ^L_k

Zakładamy, że zamiana energii w układzie zachodzi jedynie pod wpływem sił zachowawczych, tzn. gdy na składniki układu nie działają siły tarcia ani siły oporu ośrodka. Założymy również, że układ jest izolowany od otoczenia, tzn. że żadne siły zewnętrzne pochodzące od ciał spoza układu nie powodują zmian energii w obrębie układu. Gdy siła zachowawcza wykonuje pracę W nad jednym z ciał układu, zachodzi zamiana energii kinetycznej E_k dała w energię potencjalną E_p układu (lub odwrotnie).

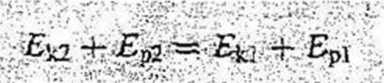
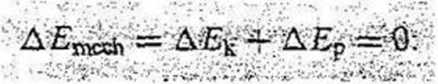
W układzie izolowanym, w którym zamiana energii pochodzi jedynie od sil zachowawczych energia kinetyczna i energia potencjalna mogą się zmieniać, lecz ich suma czyli energia mechaniczna nie może ulegać zmianie.