29031 Scan Pic0020

Rozwiązanie zadania 1.35 Prawidłowa odpowiedź: A.

Pęd ciała jestp = mu, skąd v = ~. Energia kinetyczna E tego ciała wyraża

m

się przez pęd następująco:

X 2

t = —mu = -

-m\ -

m

1 mp

~2~rrP

W

2 m

Kulki o masach m-, i m₂ mają zatem energie kinetyczne E_t i E₂ równe:

r

jl

2m

Ł-JL.

2m,

ZL

6m

Stosunek tych energii jest

a więc

e₂=-Ł-.

²    3

Rozwiązanie zadania 1.36 Prawidłowa odpowiedź: B.

Przed wystrzałem suma pędów działa i pocisku była równa zeru. Aby była spełniona zasada zachowania pędu, po wystrzale pocisk i działo muszą uzyskać pędy o jednakowych wartościach i przeciwnych zwrotach. Wartości pędów, m_pu_p pocisku i m_dv_d działa, spełniają zależność:

stąd v. = ■

Uzyskana przez działo energia kinetyczna jest

E, =~m_dv¹d =    ⁱⁿ²

^k 2 ^{d d}    2m_d

- = 2-10¹ J.

Rozwiązanie zadania 1.37 Prawidłowa odpowiedź: B.

Energia kinetyczna ciała i jego pęd są związane relacją (patrz zadanie poprzednie): zaś w chwili \ jest ona równa

ą JL

¹ 2m

Ich stosunek wynosi:

z'

Pl

thji

JŁ

i

Rozwiązanie zadania 1.38 Prawidłowa odpowiedź: D.

£,=

IL

2 m

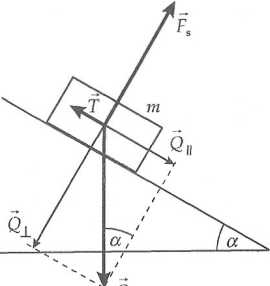
Na ciało o masie m zsuwające się po równi pochyłej działają trzy siły: ciężaru Q = mg, sprężystości podłoża_F_s i siła tarcia T. Jeżeli ciężar Q rozłożymy na składowe: równoległą do równi i prostopadłą do równi Q_x to, jak widać z rysunku, wartości tych sił będą równe:

Q_n= mg sin a

Q_± = mg cos a.

9Mwa    Q_l jest

równoważona przez siłę sprężystości podłoża F_s,

Q₁=F_S- mg cos a,

zaś wypadkowa sił Qu i T nadaje ciału przyspieszenie a wzdłuż równi. Wartość siły tarcia T jest równa T =/F_n (patrz [1], str. 50), gdzie F_n jest wartością siły nacisku ciała na równię, a/ zależnym od rodzaju trących powierzchni współczynnikiem tarcia kinetycznego. Ciało naciska na równię siłą o wartości

F„ = Q_a = mg cos a, •

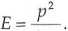
- 39 -

1

m

W chwili t₂ energia kinetyczna jest równa