Scan Pic0078

Rozwiązanie zadania 5.12 Prawidłowa odpowiedź: D.

Podane w temacie współczynniki załamania n_a i n_b to bezwzględne współczynniki załamania. Możemy je więc wyrazić jako gdzie v_a i v_b to prędkości światła w ośrodkach a i b. Prawo załamania światła na granicy tych dwóch ośrodków przyjmuje postać:

sino: _    _^b_ _ 2 _> ^

sin /? v_h n_a 1,6

Stąd wnioskujemy, że kąt padania o:musi być większy od kąta załamania /? światła na granicy obu ośrodków. Ten warunek spełnia tylko promień 4.

Rozwiązanie zadania 5.13 Prawidłowa odpowiedź: C.

Jeśli światło przechodzi z ośrodka o większym współczynniku załamania do ośrodka o mniejszym współczynniku załamania (z ośrodka optycznie gęstszego do optycznie rzadszego), to kąt załamania na granicy tych ośrodków jest większy od kąta padania. Wynika to z prawa załamania, które np. dla przejścia światła z płytki do próżni ma postać:

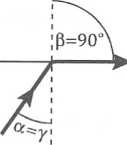
sino:    v ^    ;

sin/? c

siny _ v sin 90° c

Dla kąta padania równego kątowi granicznemu y kąt załamania/? jest równy /? = 90°, a więc

Prędkość światła w płytce obliczymy na podstawie informaqi zawartych w temacie zadania. Jeżeli promień pada na płytkę pod kątem 0°, to pzechodzi on przez nią bez zmiany kierunku i drogę Z przebywa w czasie t. A zatem prędkość światła w płytce jest równa

Stąd obliczamy:

l

t

ct

Rozwiązanie zadania 5.14 Prawidłowa odpowiedź: B.

Długość ogniskowej soczewki zależy od jej kształtu określonego przez promienie krzywizny r, i r₂, od materiału, z którego wykonana jest soczewka i od ośrodka, w którym się znajduje:

hM

i

1_\

BP

W rozważanym przypadku n jest bezwzględnym współczynnikiem załamania materiału, z którego została wykonana soczewka, a promienie krzywizn są sobie równe, b = r₂ = r. Ponadto ogniskowa / ma długość równą promieniowi krzywizny r. Podstawiając te dane do powyższego wzoru otrzymujemy:

— = (n-ijpi|    skąd n = ~.

r    r    2

Rozwiązanie zadania 5.15 Prawidłowa odpowiedź: C.

Zanim przystąpimy do rozwiązania zadania zauważmy, że względny współczynnik załamania fali na granicy dwóch ośrodków

*2/1

można wyrazić poprzez bezwzględne współczynniki załamania tych . ośrodków. Bezwzględny współczynnik załamania ośrodka 1 jest równy

skąd Uj = -

i podobnie dla ośrodka 2:

skąd v₂

Podstawiając obliczone prędkości do zapisanego wyżej wzoru na względny współczynnik załamania otrzymujemy bardzo ważny związek:

^l2/l

- 155 -