43305 Scan Pic0039

Rozwiązanie zadania 2.32 Prawidłowa odpowiedź: C.

Ciężar i siła wyporu działające na krę równoważą się wzajemnie:

W tym równaniu# jest gęstością lodu, V_k - objętością kry, p_w - gęstością wody, a V_z - objętością zanurzonej części kry. Z powyższego równania możemy obliczyć stosunek objętości kry V_k do objętości jej części zanurzonej V_z. Wynosi on:

% 1 *

Objętość części kry znajdującej się nad wodą to różnica V_k - V_z, a szukany stosunek* tej objętości do objętości jej części podwodnej V_z obliczamy następująco:

,₌M₌Ł₁₌^_₁₌I.

V_z V_{z    Pl}    9

Rozwiązanie zadania 2.33 Prawidłowa odpowiedź: D.

Gdyby w pewnej temperaturze t długości tych prętów zrównały się, to zachodziłaby równość:

skąd

l₂    1 + X_xt

Z₁ ” 1 + X₂t'

Jeśli zgodnie z treścią zadania l₂ > l_v to

i_ ₌ _ł±V__>1

Zj 1 + JL₂t    '

1 + AjZ > 1 + A.₂t/

Rozwiązanie zadania 2.34 Prawidłowa odpowiedź: D.

Energię potencjalną bryły (ciała rozciągłego) obliczamy z wzoru

E_pmtngh_c/

gdzie h_c jest wysokością środka ciężkości tej bryły. W naszym przypadku

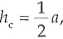
tzn. jest połową długości boku sześcianu.

Stosunek energii potencjalnej E_p sześcianu po ogrzaniu do energii potencjalnej E_p0 przed ogrzaniem wynosi

E

_p_

^Epo

— = 1 + At, ^ao

bo a = a₀ (1 + At), gdzie X jest współczynnikiem rozszerzalności liniowej sześcianu.

Rozwiązanie zadania 2.35

Prawidłowa odpowiedź: A.

Wydłużenie Al doskonale sprężystego drutu jest wprost proporcjonalne do jego początkowej długości l₀, do działającej siły F i odwrotnie proporcjonalne do pola przekroju poprzecznego S drutu:

_AT Fl₀    . F Al

Al--—,    lub inaczej---.

S    S l₀

Stały dla danego materiału współczynnik proporcjonalności E to moduł Younga

Łsft

i k

stąd

- 77 -