Scan Pic0016

Rozwiązanie zadania 1.15 Prawidłowa odpowiedź: C.

Ciało porusza się w dowolnym kierunku ruchem jednostajnym prostoliniowym, gdy siły działające na to ciało równoważą się wzajemnie. Siłę F równoważy siła F₃.

Rozwiązanie zadania 1.16 Prawidłowa odpowiedź: D.

Spoczywające początkowo ciało H = 0) pod wpływem stałej siły porusza się ruchem jednostajnie przyspieszonym z przyspieszeniem o war-r

tości a = —. Przebyta droga równa jest:

„    1 ,₂ Ft² rjr-f,

s = -zrat^Ł = —— = 750 m.

2    2 m

Rozwiązanie zadania 1.17 Prawidłowa odpowiedź: D.

-*E = mgh

^si

-E = mg(h-s₁)

E = rog(fe-s₁-s₂) s₃

E = 0

Energia potencjalna ciała spadającego swobodnie z wysokości h zależy od f” przebytej drogi s w następujący sposób:

E = mg(h- s).    ,

W trakcie spadania energia E maleje z taką szybkością, z jaką rośnie s. ----

Ponieważ ciało spada ruchem jednostajnie przyspieszonym, więc ostatni j \ odcinek drogi s₃ przebywa 7777 ono najszybciej.

Rozwiązanie zadania 1.18 Prawidłowa odpowiedź: C.

Jeśli pominąć opór powietrza, to jedyną siłą działającą na pocisk podczas ruchu jest siła ciężkości mg. Sprawdzimy na początek na jaką wysokość wzniesie się pocisk, któremu nadano zwróconą w górę prędkość o wartości 40 m-s^-1. Skorzystamy z zasady zachowania energii mechanicznej:

= mgh, stąd h = 80 m.

Obliczmy teraz potrzebny na to czas: f=t>₀-£f

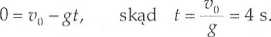
Tak więc pocisk po osiągnięciu w ciągu czterech sekund wysokości 80 m zacznie swobodnie spadać. Drogę przebytą w ciągu jednej sekundy obliczymy ze wzoru:

Zatem w ciągu pięciu sekund pocisk przebył drogę 85 m. Rozwiązanie zadania 1.19

Prawidłowa odpowiedź: B.

Warunkiem ruchu jednostajnego po okręgu jest, by wypadkowa F wszystkich sił rzeczywistych działających na ciało miała stałą wartość i zawsze była zwrócona do środka okręgu. ZII zasady dynamiki wiemy, że F = ma . Wartość wektora a jest więc stała, a jego kierunek ulega zmianie.

Rozwiązanie zadania 1.20 Prawidłowa odpowiedź: B.

Na sprężyny dolne działają siły o wartościach P_B i P_A < P_B, a więc y_q> y₂. Na każdą ze sprężyn górnych działa taka sama siła, a jej wartość jest równa P_A + P_B (ciężar samych sprężyn pomijamy). Mamy więc = x

Rozwiązanie zadania 1.21 Prawidłowa odpowiedź: C.

Pęd ciała wzrasta od wartości początkowej p₀ = mv₀ do wartości/? = nmv₀ po upływie czasu f. Przyrost pędu następuje pod działaniem siły ciężkości o wartości mg. ZII zasady dynamiki w postaci ogólnej, Ft = Ap, obliczamy:

F    F

g

^ _ Ap nmv₀ — mv₀

mo_Q(n-l) _ v₀(n-1) ^m8    g

- 31 -