Scan Pic0028

Rozwiązanie zadania 1.69 Prawidłowa odpowiedź: B.

Sygnał dźwiękowy przebył drogę równą podwójnej odległości okrętu od góry lodowej (biegł tam i z powrotem). Mamy więc:

21 = vt, stąd 1 = —vt = 1950 m.

2

Rozwiązanie zadania 1.70 Prawidłowa odpowiedź: D.

Poziom natężenia dźwięku definiowany jako (patrz [2], str. 94)

n = log—

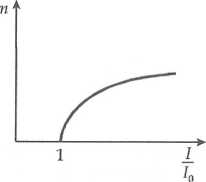
jest rosnącą funkcją natężenia I. Jeśli natężenie wzrosło od Jk = 10"¹⁰ W-m“² do I₂ = 10‘⁶ W-m“², to poziom natężenia także wzrósł.

Jeśli n_x = log — jest poziomem natężenia

i

dźwięku o natężeniu I_v a n₂ = log - —

poziomem natężenia dźwięku o natężeniu I₂, to szukany wzrost poziomu natężenia jest równy:

n₂-_Wl= log i— logi.

Różnica logarytmów dwóch liczb równa jest logarytmowi ilorazu tych liczb, a zatem

^logy-

BMji

10

n₂ -n_x = log -_iQ__l0 = loglO = 4 B = 40 decybeli.

2 Fizyka cząsteczkowa T ermo dynamika

- ZADANIA -

Zadanie 2.1

Energia wewnętrzna stałej masy gazu nie ulega zmianie w przemianie:

A. izochorycznej    B.    izotermicznej

C. adiabatycznej    D.    izobarycznej

Zadanie 2.2

Jeżeli temperatura gazu idealnego wzrosła z 7\ = T do T₂ = riT, to średnia prędkość cząsteczek tego gazu wzrosła:

A. n razy    B.    4n razy

C. n²razy    D.    2n²razy

Zadanie 2.3

Układ pobrał ciepło równe 2000 J i wykonał pracę 500 J. Zmiana jego energii wewnętrznej wynosiła:

A. 2500 J    B. 2000 J    C. 1500 J    D. 500 J

Zadanie 2.4

600 J    D. 400 J

Jeden mol gazu doskonałego rozprężając się izobarycznie pobrał 1000 J ciepła i wykonał pracę 600 J. Zmiana jego energii wewnętrznej wynosiła: A. 1600 J    B. 1000 J    C.

Zadanie 2.5

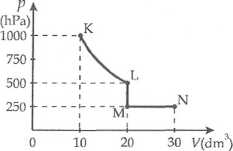
Wykres przedstawia przemiany termodynamiczne pewnego gazu. Praca wykonana przez ten gaz była:

A.    największa w przemianie KL

B.    największa w przemianie LM

C.    największa w przemianie MN

D.    taka sama w każdej z tych przemian

- 55