img027 3

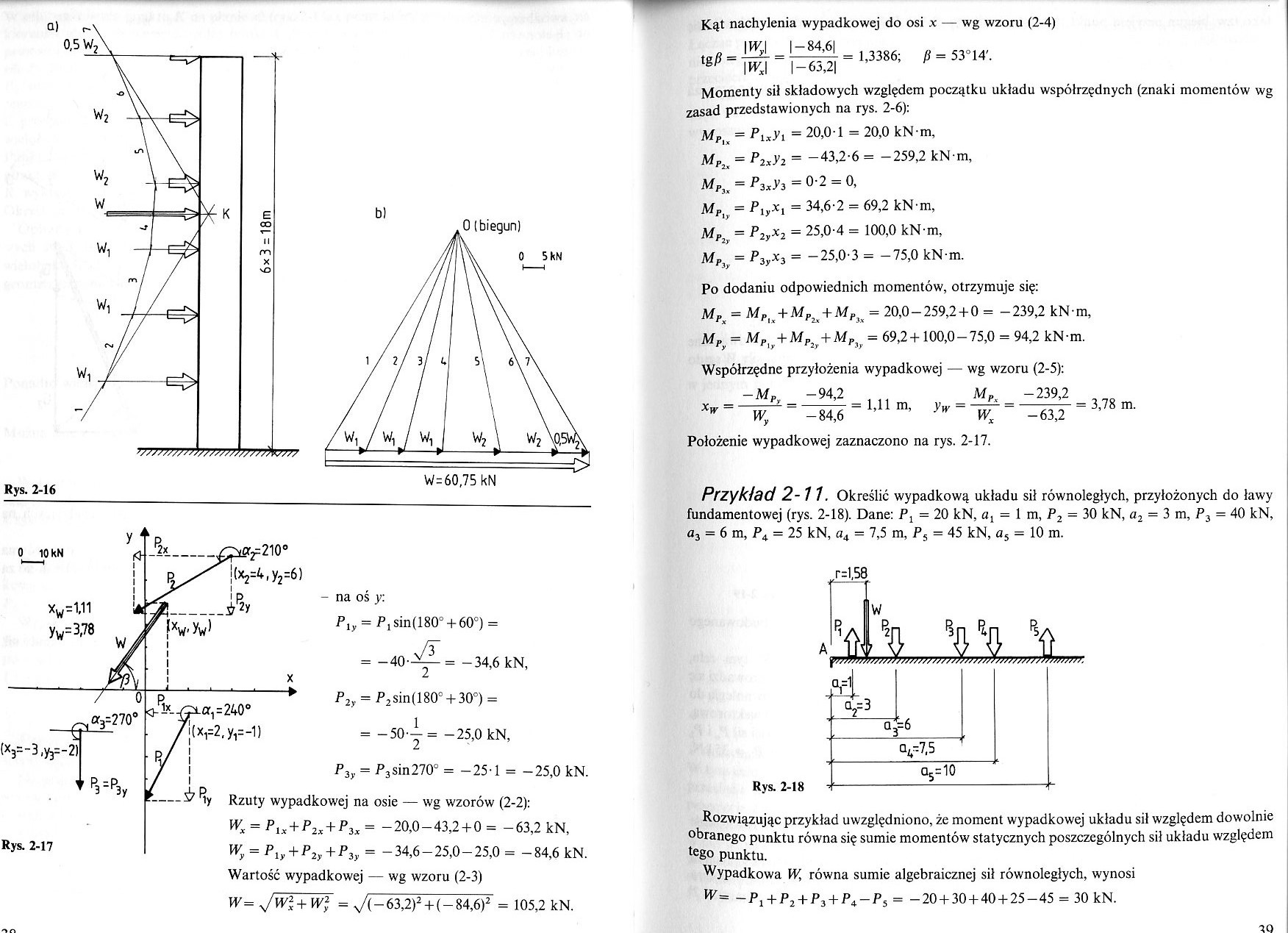
Rys. 2-16

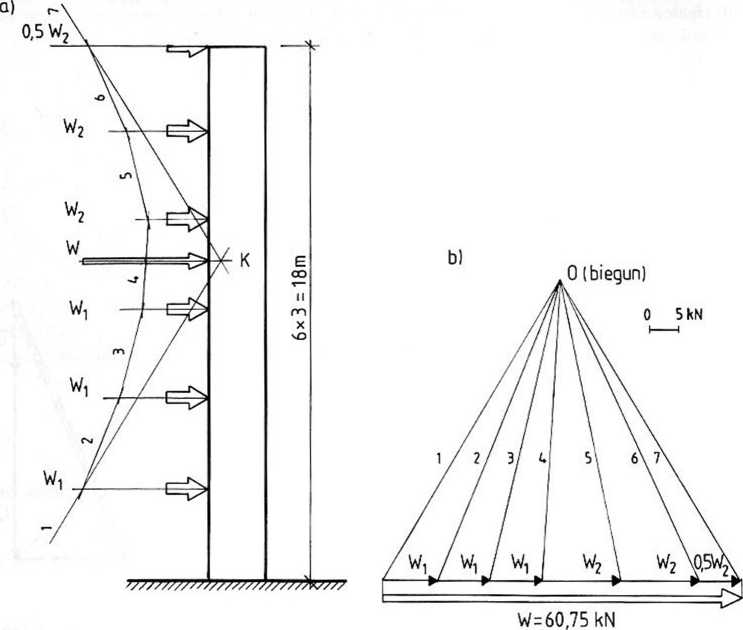
O 10 kN

-1,11 y_w=³-⁷⁸

or₃-270°

<y.lx.^Qf_{1 =} 240^o

(^xi=2, y-i=-i)

(x₃=-3,y₃=-2)

▼ ^PB=^P3y

Rys. 2-17

2x______^0^210°

(X2=4,y₂=6)

- na oś y:

P_ly= P,sin(180= + 60^c) =

_v'^/3~

= —40-^— = -34,6 kN,

P_2y = P₂sin(180^c + 30°) =

= -50 y = -25,0 kN,

P_3y = P₃sin270° = -25-1 = -25,0 kN.

^----^ Rzuty wypadkowej na osie — wg wzorów (2-2):

W_x = P_lx + P_Zx + P_3x = -20,0-43,2 + 0 = -63,2 kN,

W_y = P_ly + P_2y + P_3y = -34,6-25,0-25,0 = -84.6 kN. Wartość wypadkowej — wg wzoru (2-3)

W= s/wl+wj = s/( — 63,2)² + (— 84,6)² = 105,2 kN.

\W_X\ |-65,2|

Kąt nachylenia wypadkowej do osi x — wg wzoru (2-4) = 1,3386; [i = 53°14'.

\W_y\ |-84,6| *8^ ⁼ W? ⁼

Momenty sil składowych względem początku układu współrzędnych (znaki momentów wg zasad przedstawionych na rys. 2-6):

M_P|i = P_ixyi = 20,0-1 = 20,0 kN-m,

M_P; = P_2xy₂ = -43,2-6 = -259,2 kN-m,

Mp_ix = P_3xy₃ ⁼ 0‘2 = o,

M_Pu = P_{yXi = 34,6-2 = 69,2 kN-m,

M_Ply = P_2y^x2 = 25,0-4 = 100,0 kN-m,

M_P}y = P_3yx₃ = -25,0-3 = -75,0 kN-m.

Po dodaniu odpowiednich momentów, otrzymuje się:

M_P =M_P +Mp +Mp = 20,0-259,2 + 0 = -239,2 kN-m,

Mp=M_P +M_P +M_P = 69,2+100,0-75,0 = 94,2 kN-m.

i ..    * l it    r 5%,    * lii

Współrzędne przyłożenia wypadkowej — wg wzoru (2-5):

Xur — ‘

-M_P, -94,2

— 1,11 m, y_w = ■

M

Px

W_r

-84,6

Położenie wypadkowej zaznaczono na rys. 2-17.

-239,2

-63,2

= 3,78 m.

Przykład 2- 1 7. Określić wypadkową układu sil równoległych, przyłożonych do ławy fundamentowej (rys. 2-18). Dane: P_: = 20 kN, aj = 1 m, P₂ = 30 kN, a₂ = 3 m, P_} = 40 kN, a₃ = 6 m, P₄ = 25 kN, a₄ = 7,5 m, P₅ = 45 kN, a₅ = 10 m.

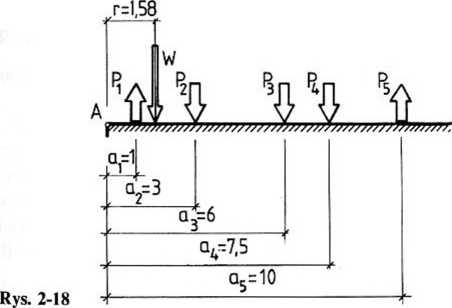
Rozwiązując przykład uwzględniono, że moment wypadkowej układu sił względem dowolnie obranego punktu równa się sumie momentów statycznych poszczególnych sił układu względem tego punktu.

Wypadkowa W, równa sumie algebraicznej sił równoległych, wynosi -P₁+P₂+P₃ + P₄-P₅ = -20 + 30 + 40 + 25-45 = 30 kN.