Kondensator PE 63

1.8.3. Połączenia kondensatorów 63

1.8.3. Połączenia kondensatorów 63

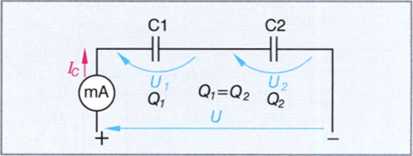
Rys. 1. Połączenie szeregowe kondensatorów

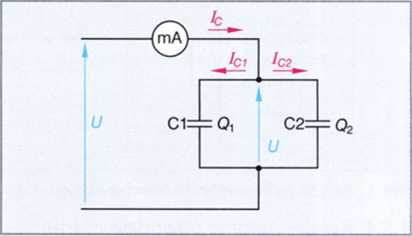
Rys. 2. Połączenie równoległe kondensatorów

1.8.3. Łączenie kondensatorów

Połączenie szeregowe

W szeregowym połączeniu kondensatorów wypadkowy ładunek jest mniejszy niż w przypadku pojedynczego kondensatora dołączonego do tego samego źródła napięcia, ponieważ przy połączeniu szeregowym na każdym kondensatorze odkłada się tylko część napięcia zasilającego.

W połączeniu szeregowym kondensatorów zastępcza pojemność jest zawsze mniejsza od pojemności najmniejszego kondensatora.

Ładunek dostarczony do kondensatorów połączonych szeregowo jest taki sam. Suma napięć na kondensatorach jest równa napięciu zasilania: U = L/, + U₂ (rys. 1). Wobec tego napięcia na kondensatorach muszą być odwrotnie proporcjonalne do pojemności, aby kondensatory mogły przyjąć jednakowe ładunki.

W połączeniu szeregowym kondensatorów odwrotność pojemności zastępczej jest równa sumie odwrotności pojemności kondensatorów składowych.

Przykład 1:

Dwa kondensatory 270 pF i 470 pF są połączone szeregowo. Jaka jest pojemność zastępcza?

Rozwiązanie:

C, • C₂ _ 270 pF • 470 pF " C, + C₂ “ 270 pF + 470 pF

171,5 pF

Połączenie szeregowe:	Połączenie szeregowe dwóch
	kondensatorów:
U = U, +u2
	0 C1 C2
1 1 1	c, • Co
	c - ^1 2
c c, c2	c, + c2

Połączenie równolegle:

O = O, + Oj

=> C U = C, U + C₂ U

C = C, + C₂ + ...

Przykład 2:

Wypadkowa pojemność dwóch kondensatorów połączonych szeregowo jest równa 248 pF. Jeden z kondensatorów ma pojemność C, = 680 pF. Jaka powinna być pojemność drugiego kondensatora?

Rozwiązanie:

1-J- —    ₌

C~ C, C₂ ^ C₂~ C C,

=-2l2l = ^24S P^F • ⁶⁸⁰ P^F _ 390 pF ² C,-C 680 pF - 248 pF

C pojemność zastępcza;    C,, C₂ pojemności składowe

W połączeniu równoległym kondensatorów pojemność zastępcza jest równa sumie pojemności składowych.

Połączenie równoległe

W połączeniu równoległym ładunek wypadkowy, a więc także pojemność zastępcza, jest większy od każdego z kondensatorów.

Na kondensatorach połączonych równolegle jest takie samo napięcie (rys. 2). Ładunek całkowity jest równy sumie ładunków obydwu kondensatorów, czyli 0 = 0, +Q₂. A ponieważ pojemności są proporcjonalne do ładunków, więc C = C, + C₂.

Przykład 3:

Trzy kondensatory 470 pF, 270 pF i 68 pF połączono równolegle. Jaka jest pojemność zastępcza?

Rozwiązanie:

C = C, + C₂ + C₃ = 470 pF + 270 pF + 68 pF = 808 pF

Pojemności zastępcze mieszanych połączeń kondensatorów oblicza się krok po kroku, wyznaczając kolejno pojemności zastępcze poszczególnych gałęzi, w których elementy są połączone szeregowo albo równolegle.