Kondensator PE 64

64 1.8.4. Kondensator w obwodzie prądu statego

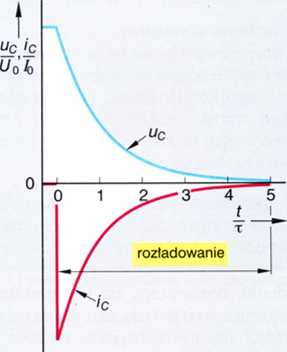
Rys. 1. Krzywe ładowania i rozładowania kondensatora

1.8.4. Kondensator w obwodzie prądu stałego

Gdy połączymy kondensator ze źródłem napięcia statego, popłynie krótkotrwały prąd ładowania. Po naładowaniu kondensatora prąd przestaje płynąć.

Naładowany kondensator przerywa przepływ f prądu stałego.

Jeśli kondensator jest ładowany przez rezystor szeregowy, napięcie na kondensatorze z początku szybko, a potem coraz wolniej rośnie, aż do osiągnięcia wartości ustalonej (rys. 1). Podczas rozładowania napięcie z początku szybko, a potem coraz wolniej maleje do wartości 0 V. Prąd ładowania lub rozładowania w chwili załączenia napięcia zasilania skokowo rośnie do wartości początkowej, a później, z początku szybko, a potem coraz wolniej maleje do zera. Przebiegi czasowe prądów i napięć przy ładowaniu i rozładowaniu nazywamy przebiegami nieustalonymi i są one funkcjami wykładniczymi.

Czasy ładowania i rozładowania są tym większe, im większa jest rezystancja szeregowego rezystora i pojemność kondensatora.

Iloczyn rezystancji i pojemności nazywa się stalą czasową x.

Stała czasowa jest to czas, po którym napięcie podczas ładowania kondensatora osiąga 63,2% wartości ustalonej, a przy rozładowaniu 36,8% wartości początkowej. Po upływie czasu równego 5t proces ładowania lub rozładowania jest praktycznie zakończony (rys. 1).

Początkowa wartość prądu przy ładowaniu i rozładowaniu jest ograniczona tylko przez rezystancję obwodu.

o"^ą II ^53 l°^c	O QC II P
[T] = Q . F= )L . = s A V Podczas ładowania kondensatora (nie naładowanego):
uc = U0- [1 -e ^Vt]	ic = lo ■ e-*
Podczas rozładowania kondensatora (naładowanego):
uc = U0- e-**	iC = ^!o ■ ^e~^Vx

wartość początkowa natężenia prądu U₀    napięcie źródła zasilania, wartość ustalona

napięcia na kondensatorze R    rezystancja obwodu

x    stała czasowa (grec. litera tau)

C    pojemność

u_c    chwilowa wartość napięcia

na kondensatorze t    czas

i_c    chwilowa wartość prądu ładowania

lub rozładowania

Przykład:

Kondensator o pojemności 470 pF jest dołączony do źródła napięcia przez rezystor 100 kU. Jaka jest stała czasowa?

Rozwiązanie:

_T = R • c = 100 k£2 • 470 pF = 47 uS