Kolendowicz'1

2. Rama utwierdzona. Współczynniki m_B'\m_Ez tabl. 12-2:

m_B = — 0,056,    m_E = 0,069.

Momenty zginające (wg (12-12), (12-15) i (12-16)) są: M_b = mgql² = — 0,056 • 40 ■ 6² = — 80,64 kNm, M_e = mrfl¹ = 0,069 • 40 • 6² = 99,36 kNm,

1    1

M_a = -~M_b = --(-80,64) = +40,32 kNm. Reakcje (wg (12-17) i (12-18)):

= 30,24 kN,

3 A/„    3 80,64

~ 2 h ~ 2    4

V =

ql 40-6

= 120 kN.

■    Wykres momentów zginających przedstawiono na rys. 12-12d.

■    Z porównania wartości momentów zginających dla obu ram, przegubowej i utwierdzonej, wynika, że utwierdzenie słupów wpływa na zwiększenie momentu w węzłach narożnych B i C i równocześnie zmniejszenie momentu dodatniego w ryglu.

■    W ramie utwierdzonej reakcja pozioma H jest prawie dwukrotnie większa od reakcji poziomej w ramie przegubowej, co decyduje (oprócz momentu utwierdzenia) o wielkości fundamentów.

12.4. Ramy statycznie niewyznaczalne o węzłach przesuwnych

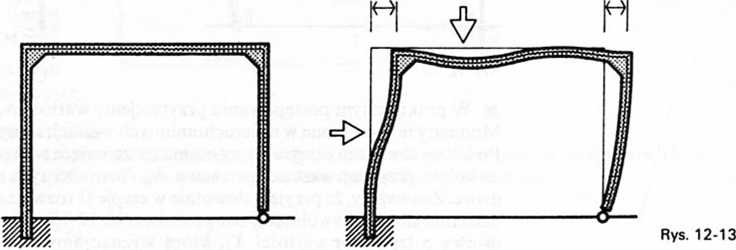
Rama pokazana na rys. 12-13a jest ramą o węzłach przesuwnych. Przy dowolnym obciążeniu, symetrycznym i niesymetrycznym, nastąpi obrót i przesuw węzłów (rys. 12-13b). Ramę tę rozwiązujemy sposobem Crossa w dwóch etapach. W pierwszym etapie uniemożliwiamy przesuw węzłów przez wprowadzenie dodatkowej podpory (rys. 12-14a) i obliczamy momenty zginające. W wyniku jednak dodatkowego podparcia tej ramy, na dodatkowej podporze wystąpi reakcja R. W etapie tym można więc traktować ramę jako obciążoną siłami rzeczywistymi oraz siłą skupioną R uniemożliwiającą przesuw (rys. 12-14b). W rzeczywistości jednak podpora dodatkowa nie istnieje i nie istnieje siła pozioma R, której działanie w etapie pierwszym rozwiązywania ramy należy zlikwidować. Czynimy to w etapie drugim, gdzie usuwamy wprowadzoną dodatkową podporę i obciążamy ramę siłą X = R przeciwnie skierowaną do R (rys. 12-14c). Przesunięcie węzłów, jakie teraz nastąpi, wywoła zgięcie prętów ramy, a więc tym samym wystąpienie momentów zginających, które należy dodać do momentów obliczonych w etapie pierwszym. Rozwiązanie ramy w etapie drugim polega zatem na wyznaczeniu momentów zginających wywołanych tylko przesuwem węzłów.

a)    b) a    A

271