lastscan16

Chcąc natomiast spłacić 1500 zł kwotą 1600 zł, jeśli d = 10%, należałoby dokonać spłaty po upływie czasu obliczonego według wzoru (2.6),

n

100

1600 0.1

= 0,625 roku.

czyli za 7,5 miesiąca.

■

Przykład 2.3

Pod koniec 2001 r. dużą popularnością cieszyły się w naszym kraju tzw. lokaty anty podatkowe z odsetkami płatnymi z góry, oferowane przez banki w związku z wprowadzanym 20-procentowym podatkiem od odsetek. Rozpatrzymy sytuację klienta, który zamierzał wówczas ulokować 10 tys. zł na pół roku w jednym z banków:

•    w banku X proponującym półroczną lokatę z odsetkami płatnymi z góry, obliczanymi przy stopie d = 12%,

•    w banku Y proponującym tradycyjną lokatę z oprocentowaniem r = 15%. Gdyby klient zdecydował się na lokatę w banku X, to po upływie pół roku

miałby kwotę

10638,30 zł.

P    10000

1 —dn ~ 1-0,12 0,5

czyli uzyskałby z lokaty F—P = 638,30 zł. nie płacąc od tego podatku. Gdyby wybrał bank Y, to wartość półrocznych odsetek wynosiłaby

I = Pm = 10000 0,15 0.5 = 750 zł.

Jednakże skoro odsetki zostałyby obciążone 20-procentowym podatkiem, to w efekcie uzyskałby tylko 750 —750 0,2 = 600 zł. Jak widać, „antypodatkowa" lokata w banku X była korzystniejsza niż tradycyjna lokata w banku Y.

Sprawdzimy jeszcze, przy jakim oprocentowaniu w banku Y obie lokaty byłyby dla klienta jednakowo korzystne. Rozwiązujemy w tym celu równanie względem r,

10000- r- 0,5 0.8 = 638,30,

w którym po lewej stronie znajduje się wartość półrocznych odsetek od lokaty w banku Y po opodatkowaniu (współczynnik 0.8 zmniejsza kwotę odsetek o 20%). po prawej stronie zaś odsetki w banku X. Rozwiązaniem tego równania jest stopa r = 15,96%. zatem tradycyjna lokata w banku Y byłaby dla klientów’ równie korzystna jak „antypodatkowa” lokata w banku X dopiero przv oprocentowaniu 15,%% p.a.

Powróćmy teraz do założenia D < F, które po uwzględnieniu wzoru (2.2) przyjmuje postać nierówności

Fdn < F.

Wynika stąd. że stopa dyskontowa d i czas pożyczki n musza spełniać nierówność

dn<\.    (2.7)

Założenie (2.7) oznacza, że:

•    przy danej stopie d dyskonto D można obliczyć tylko dla czasu

1

|

•    przy danym czasie n dyskonto D można obliczyć tylko dla stopy

■

n

•    oba te warunki dotyczą pożyczki w dowolnej wysokości F > 0. Dodatkowy komentarz do powyższych w niosków jest związany z rysunkiem 2.3.

który przedstawia początkową kwotę P jako funkcję czasu n daną równaniem (2.3). Jest to funkcja liniowa, która dla n = 0 przyjmuje wartość F; wraz ze wzrostem n wartości tej funkcji maleją i osiągają wartość 0 wtedy, gdy F( 1 — dn) = 0, czyli gdy dn = 1. Ponieważ jednak pożyczka ma sens tylko przy P > 0, omawiana funkcja nic jrjcst określona dla n ^ Md, co jest równoważne założeniu (2.7).

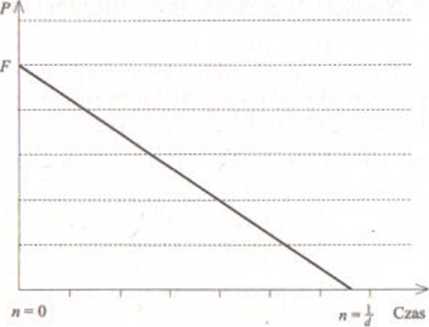
Rysunek 2.3. Wartość początkowa P jako funkcja czasu n

Model (2.2H2.3) budowaliśmy w celu formalnego opisu pożyczki z opłatą mającą postać dyskonta, lecz stanowi on także formalny opis dyskontowania weksli. Jeżeli bowiem przedstawiając weksel do dyskonta, znamy jego wartość nominalną F, czas do wykupu n oraz stopę d proponowaną przez bank. to model bezpośrednio służy do obliczenia dyskonta l) oraz wartości aktualnej weksla P. Ale np. przy zakupie bonów skarbowych model ten służy do innego celu. ponieważ kupując bon. proponujemy jego cenę P, znając wartość nominalną F i czas do jego