lastscan84

Zamiana renty uogólnionej na równoważną rentę prostą przez zmianę raty

Typ I: R =-, n = n_Qm_K, i = p.

Typ II: R =    n = —, i = p.

gdzie /₀ = (1 +p)^Vm•- I.

W rozpatrywanych do tego miejsca rentach uogólnionych zakładaliśmy, ż( w podokresach odsetki naliczane są zgodnie z zasadą oprocentowania składanego Dzięki temu wyceniając rentę na początek lub koniec renty, lub na dowolnj moment uiszczenia raty, lub na dowolny moment kapitalizacji odsetek, otrzymujemj spójne wyniki, gdyż operujemy kapitałami równoważnymi.

W praktyce jednak renta uogólniona typu II wiąże się niejednokrotnie z innymi sposobami naliczania odsetek w podokresach. Jednym z nich jest stosowanie oprocentowania prostego według stopy proporcjonalnej.

Przykład 5.16

Powróćmy do renty z przykładu 5.l4(c). zakładając tym razem, że odsetki za podokresy naliczane są zgodnie z zasadą oprocentowania prostego - według stopy proporcjonalnej, a więc równoważnej dla tej zasady. Dla tego przypadku rozpatrzmy cztery raty wpłacone w pierwszym roku. Z tytułu tych wpłat na koniec roku saldo rachunku wyniesie

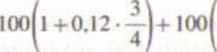
1 +0.12 • —

i)+.Oo(l+O.I2j)

+ 100 = 418 zł.

0    taką też kwotę wzrośnie saldo rachunku na koniec każdego roku jedynie z tytułu wpłat w tymże roku. Pokazaliśmy tym samym, że wartość końcowa rozważanej renty równa jest wartości końcowej renty prostej, dla której n = 4, R = 418.

1    = 12%. Zgodnie z wzorem (5.6) otrzymujemy F = 1997.76 zł.

Zauważmy, że gdyby za podokresy naliczane były odsetki zgodnie z zasadą jednolitego oprocentowania wykładniczego, co w tym przypadku równoważne jest kwartalnej kapitalizacji odsetek przy stopie 2,874%, to - jak pokazaliśmy w przykładzie 5.15 - równoważna roczna rata wyniosłaby 417.58 zł. a wartość końcowa renty 1995.73 zł. Mniejsza wysokość raty i wartości końcowej renty nie powinna dziwić, gdyż (por. rozdział 3) odsetki proste za czas krótszy od okresu kapitalizacji są większe od odsetek składanych.

■

Wycenę renty uogólnionej typu II w przypadku naliczania odsetek prostych za podokrcuy możemy przeprowadzić - jak w przykładzie 5.16 - za pomocą renty ■OMci o okresie bazowym równym wyjściowemu okresowi kapitalizacji. Zalewana wówczas zostaje wartość stopy procentowej, natomiast modyfikacjom Hdtiane są wysokość rat i ich liczba. Skumulowaną ratą końcową nazwiemy Łktualizowaną na koniec okresu kapitalizacji łączną wartość rat płaconych ■ tymże okresie. W rozważanym przypadku renty uogólnionej dana jest ona wzorem

*o"l (l + ~U

i-o \

m_B-\

Bry daje się zapisać w’ prostszej postaci, a mianowicie

)mocą skumulowanej raty końcowej możemy wycenić rentę na jej moment >wy. W tym celu wystarczy posłużyć się wzorem (5.6), przyjmując

(5.30)

■*= #io oraz i = p.

Wartości początkowej omawianej renty uogólnionej nie możemy jednak Obliczyć przez aktualizację wartości końcowej na moment 0. gdyż w przypadku itosowania oprocentowania prostego z równoważności kapitałów w momencie Inie wynika ich równoważność w innym momencie f (por. punkt 4.3). Stwarza to istotny problem w w^fycenie renty i stawia pod znakiem zapytania zasadność )wania oprocentowania prostego w podokresach. W celu obliczenia wartości jtkowej renty najpierw dla każdego okresu kapitalizacji sumujemy wartość rat lalizowanych na początek tegoż okresu. Sumę taką określimy mianem lutowanej raty pinzątkowej. Dla pojedynczego okresu kapitalizacji skumu-rana rata początkowa wyraża się wzorem

/

1+— I

-i

tępnie. przyjmując

*«*ol(l + — /) .    (5.31)

u — rio/m_B oraz i = p we wzorze (5.8), możemy obliczyć wartość początkową renty.

Przykład 5.17

Obliczmy wartość początkową renty z przykładu 5.16 na podstawie wzorów (5.31) i (5.8). Wobec ł^, = 100. m_B = 4, n₀ = 16. i' = 12%, zaktualizowana na Ipoczątek roku łączna wartość wpłaconych w tymże roku rat wynosi - zgodnie / wzorem (5.31) - 372.46 zł. Zatem dla / = 12%. n * 4 i R = 372.46 otrzymujemy

177