mech2 136

■-aaBg,-

$3 :4

270

stąd

71 D

^{W =} -3U »

15 lK G - Q = ^    —ST* •

nn r

Zwrot wektora    zaznaczono na rys. 196 zakładając G > Q.

Zadanie 12

Na osi 00 są osadzone obrotowo dwa Jednakowe krążki, z których, każdy ma moment bezwładności I względem osi 00. Oś 00 obraca się w płaszczyźnie poziomej dokoła pionowej osi 0^0-| z prędkością kątową uii, krążki zaś toozą się bez ślizgania po płaszczyźnie poziomej. Obliczyć dodatkowy nacisk krążków na płaszczyznę, będący wynikiem efektu żyroskopowegoj_a_ żeli oś 0^0-1 dzieli odległość między krążkami na połowy,promień zas każdego z krążków wynosi r,

I to?

Odp. E — p_v

3.8. Praca i energia

271

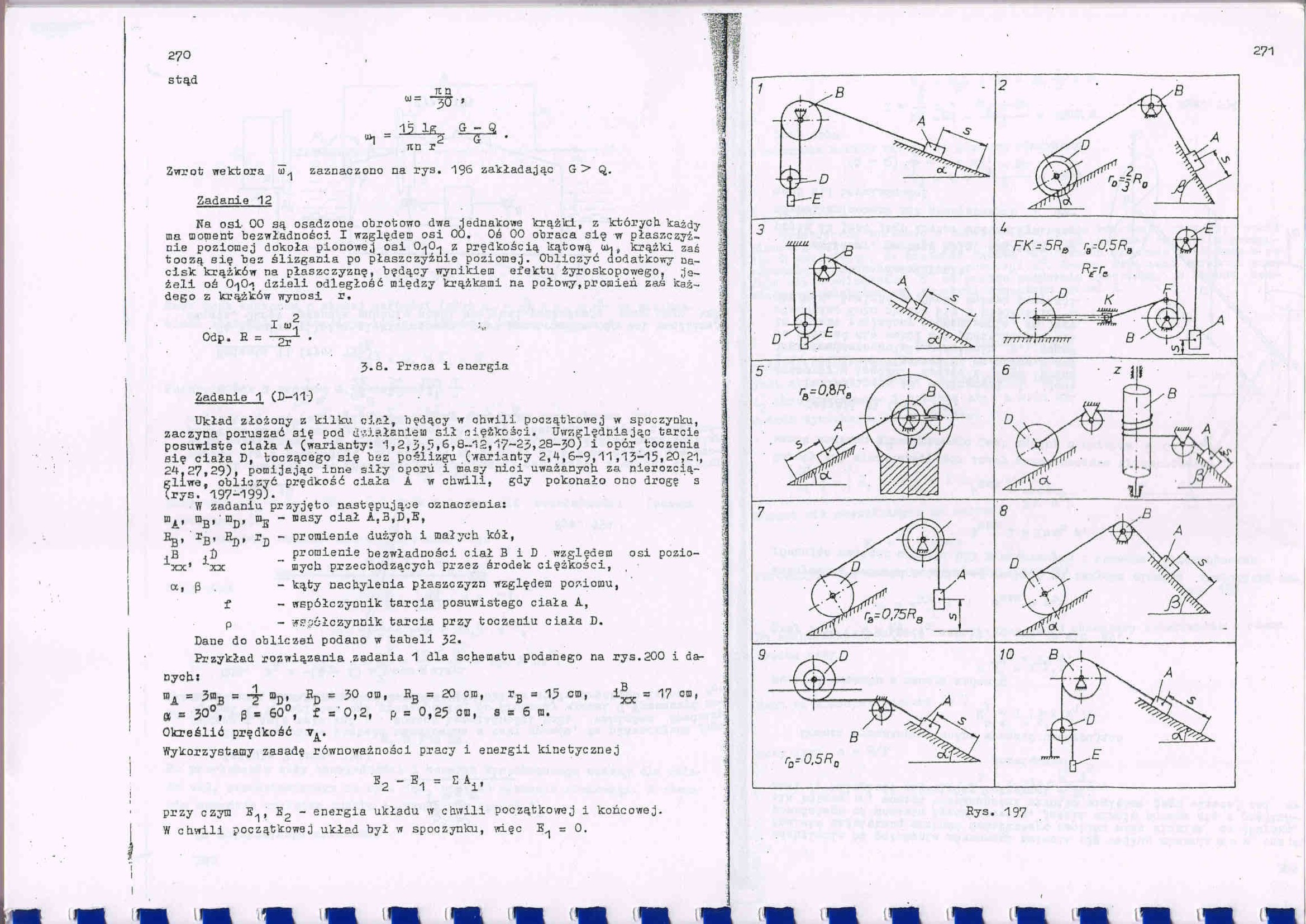
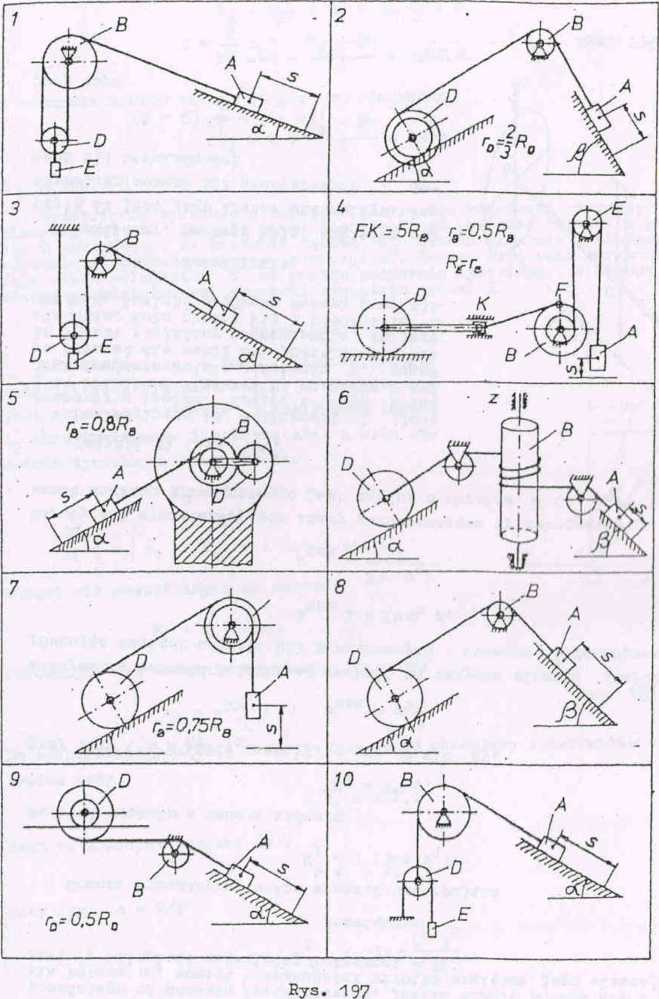
Zadanie 1 (D-11)

Układ złożony z kilku cia3 zaczyna poruszać 3ię pod dżJ

posuwiste ciała A (warianty: .......    ......

się ciała D, boczącego się buz poślizgu (warianty 2,4,6-9,11,13-15,20,21, 24.27,29), pomijając inne siły oporu i masy nici uważanych, za nierozcią-

fllwe, obliczyć prędkość ciała A w chwili, gdy pokonało ono drogę s rys. 1.97-199).

W zadaniu przyjęto następujące oznaosenia:

Dn, m^ - masy olał A,3,D,E,

- promienie dużyoh i małych kół,

promienie bezwładności ciał B i D wzglądem mych przechodzących przez środek ciężkości,

- kąty nachylenia płaszczyzn względem poziomu, f    - współczynnik tarcia posuwistego ciała A,

p    - współczynnik tarcia przy toczeniu ciała D.

Dane do obliczeń podano w tabeli 32.

Przykład rozwiązania .zadania 1 dla schematu podanego na rys.200 i danych:

^roA ⁼    = -*r Dpi Hjj = 30 om, Eg = 20 cm, ^rg = 15 cm,

$ = 30°,    (3 = 60°, f = 0,2, p = 0,25 on, s = 6 n.

Określić prędkość

Wykorzystamy zasadę równoważności pracy i energii kinetycznej

mA,	mB,i
’	^rB ’ ^J
i^B ,	i i^fl
■XX.'	^1 XX
a,	P •

osi pozio-

1^ = 17 »,

^E2 - ^E1 =

E A.

przy czym E^, E₂ - energia układu w chwili początkowej i końcowej. W chwili początkowej układ był w spoczynku, więc = 0.

<!

i

r