24
40 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków
stąd
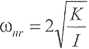
71(2/2-1) 4 r
(5.13)
Aby sprawdzić, jak odległe od wartości pulsacji obliczonych z równań różniczkowych cząstkowych (5.8) są pulsacje obliczone dla' układu przybliżonego dyskretyzacją (5.13), wprowadźmy pojęcie błędu odwzorowania definicją:
8
%
co
11--Ł 1100%
l “»J
Zauważmy, że K = k— oraz I — J—, zatem: L r
|
4 |
K ■ 1 — sm / | |
i - —i 1 Ł d ^ |
|
nr: / TT 2 |
Ti(2n -1) |
sini
j_ 4 r n{2n -1) 4 r
stąd ostatecznie
£o/„ = 1
I 7t(2n -1) \ 4r , n(2n -1) ~4r
(5.14)
Jak należało się spodziewać, wraz zc wzrostem r maleje błąd odwzorowania. W rezultacie gdy r zmierza do nieskończoności, błąd odwzorowania zmierza do zera.
W celu zobrazowania skuteczności odwzorowania pulsacji własnych wału ciągłego pulsacjami układu złożonego z elementów skupionych zostanie sporządzona tabela dla r równego 5 i 10.
|
r |
n |
1 |
2 |
3 |
4 |
5 |
6 |
|
5 |
£% |
0,41 |
3,66 |
9,97 |
18,97 |
30,14 |
42,84 |
|
10 |
e% |
0,1 |
0,92 |
2,55 |
4,96 |
8,12 |
11,98 |
Jak wynika z powyższej tabeli, system inercyjno-sprężysty złożony z dziesięcii elementów pozwala na odtworzenie z techniczną dokładnością i przybliżenie sześciu pierwszych pulsacji układu ciągłego, natomiast przy pięciu elementacl techniczna dokładność dotyczy zaledwie trzech pulsacji.
Obecnie rozważymy pulsacje własne takiego samego wału mechanicznego, jednak na jego swobodnym końcu niech znajduje się skupiony dodatkowy momeni bezwładności o wartości Jz. Tam też niech będzie przyłożony moment dany funkcją Tm j sin(coO-
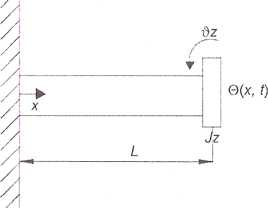
Rys. 11. Wał jednostronnie sztywno zamocowany z dodatkowym momentem bezwładności na przeciwległym końcu
Zgodnie z wyrażeniem (5.7) wał mechaniczny będzie pod wpływem przemiennego momentu skręcającego ulegał odkształceniu:
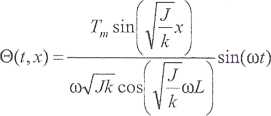
zatem
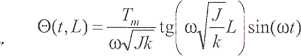
Dodatkowy moment bezwładności musi spełniać równanie dynamiki:
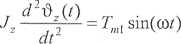
Wyszukiwarka
Podobne podstrony:
42 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków stąd dla zerowych warunków początkowych
126 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków Współczynnik przenoszenia p dla
48 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków Teraz wyrażenie (6.5) wynikające z drugi
34 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków przy warunkach brzegowych: ©0,0) = 0
A.S. Jagiełło, Systemy elektromechaniczne dla elektryków Relacja (2.2) pozwala napisać wyrażenie na
U) A,S. Jagiełło, Systemy elektromechaniczne dla elektryków Wielkości W i stanowią ogólny zapis sił
IX A S Jagiełło, Systemy elektromechaniczne dla elektryków Przebieg strat na styku koło-szyna przeds
22 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków Dla wyznaczenia macierzy sztywności
24 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków 24 A.S. Jagiełło, Systemy elektromechani
A.S. Jagiełło, Systemy elektromechaniczne dla elektryków Ostatecznie więc pulsacja własna maszyny
28 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków dla obydwu zmiennych stają się niezależn
30 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków Rys. 7. Charakterystyka rezonansowa siln
38 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków Zauważmy, że: ( eya + e~- a Y l 2 J cos3
52 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków L<t 0 VF«,1. , * .
58 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków VI
66 A.S. Jagiełło, Systemy elektromechaniczne dla elektrykówNa rysunku 18, w kolejności od dołu, zazn
70 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków 70 A.S. Jagiełło, Systemy elektromechani
więcej podobnych podstron