13

IX A S Jagiełło, Systemy elektromechaniczne dla elektryków

Przebieg strat na styku koło-szyna przedstawiono na rysunku 3.

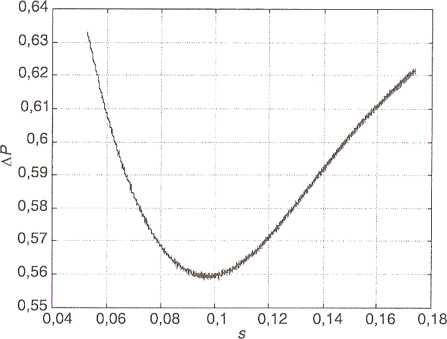
Rys. 3. Przykładowy przebieg strat powstających na styku koło-szyna

Wartości liczbowe na osi rzędnych przedstawione na rysunkach 2 i 3 są uzależnione od przyjętych danych i jako takie nie mają znaczenia absolutnego.

3. ZESPOLONA MACIERZ SZTYWNOŚCI I PODATNOŚCI DYNAMICZNEJ

W większości układów elektromechanicznych wyrażenie na koenergię kinetyczną można zapisać w postaci:

E_KoĄq^TKq + Hq (3.1)

Aby wyrażenie mogło opisywać pewną rzeczywistość fizyczną lub techniczną, macierz A winna być macierzą dodatnio określoną. Teraz można nadać macierzom A i B konkretną interpretację fizyczną. W układach i systemach elektrycznych elementy macierzy A są indukcyjnościami własnymi i wzajemnymi, a macierzy B są strumieniami skojarzonymi pochodzącymi od strumienia remanencji (pozostałości magnetycznej). W układach mechanicznych natomiast elementy macierzy A są masami lub momentami bezwładności, natomiast macierz B nie ma tu odpowiednika.

Energia potencjalna ma analogiczną strukturę:

£„=t_?^rK? + G q(3.2)

Dla układów mechanicznych elementami macierzy K są współczynniki sprężystości elementów odkształcanych, natomiast elementem macierzy G jest przyspieszenie wynikające z grawitacji. W układach elektrycznych elementami macierzy K są odwrotności pojemności, natomiast macierz G nie ma tu odpowiednika. Załóżmy teraz, żc współrzędne występujące w relacjach (3.1) i (3.2) są od siebie liniowo niezależne, a funkcja Lagrange’a ma postać:

L=K_Ko-E„    (3.3)

to po podstawieniu wyrażenia (3.3) do równania Lagrange’a drugiego rodzaju (2.3) otrzymamy:

In

di

IL*».

i b

" Jj

i j	\<łl		V		\K
i * ! !		-i-	'
	\ <łn		Sn i		kl

(3.4)