33

58 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków

VI    VI    VI

cos(pi3)    cos[pi^--|7r)    cos[p^-j7x)

-sin(/?fl)    -sin(p$-y7i;)    -sin(ptł-y7i)

natomiast dla prądów i napięć wirnika macierz transformacji Clarka:

r i		i	1
f3	VI	VI	VI 1
J n	1	~2	1 2
V z	0	VI	VI
		2	2 _

Model matematyczny maszyny indukcyjnej trójfazowej zapisanej z wykorzystaniem powyższych przekształceń ma następującą postać (patrz rozdział 15, równania (15.13)) - równania dla obwodów stojana:

CLas +    + L_m^— ptfca, + L_m)lq + L_m /p ]+ R_sId = ^> U ph COs((M ~ P&)

(8.la)

(Los + ^L^rj^^+Lm~J^ ⁺ P^\iLos + L_m)ld + Lm F_a]+R_sI_q = S U _ph sin(c0/ - p-d)

(8.Ib)

Równania dla obwodów wirnika:

(8.1c)

(8-ld)

(_r, , , \^dF_a ,_T dl_d [L_Qw+_Lm)— ^Lm~dT ^R'» ^U«

(r, ,_r )^dĄ , _T dl_q

¹ L°^{w Ln,)}~di~ ^Lm~dT ^R- ą- ą

W powyższym układzie równań pominięto równania dla składowych zerowych, natomiast układ ten musi być uzupełniony o równanie mechaniczne:

(8.1e)

O ile wybór układu odniesienia (d, q\ a, (3) jest najkorzystniejszy dla silników pomocniczych, o tyle dla silników głównych nie musi być zastosowany. Jednak zc względu na pewną unifikację analizy również w wypadku silników głównych pozostaniemy przy takim samym zapisie. Aby możliwe było rozróżnianie, który silnik jest w danej chwili analizowany, konieczne jest dodatkowe indeksowanie. I tak, indeksem p oznaczymy wielkości związane z silnikami pomocniczymi, natomiast indeksem g - z silnikami głównymi. Ponieważ jednak zmienne poszukiwane, takie jak składowe prądu mogą być różne dla różnych silników, dla tych wielkości potrzebne będzie indeksowanie podwójne i w tym przypadku będą to cyfry. Ze względu na to, że położenie kątowe wirników pary silnik główny-silnik pomocniczy jest identyczne, zatem wystarczy dla tych zmiennych pojedyncze indeksowanie cyfrowe.

Obecnie skupimy naszą uwagę na silnikach pomocniczych. Równania prądowo--napięciowe dla obwodów wirnika pierwszego z silników, po uwzględnieniu indeksowania, mają postać:

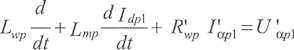
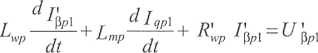
natomiast dla drugiego z nich następującą:

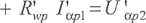
r ^dl'opl , _T ^d Idpl

^WP dt ^U'^P di

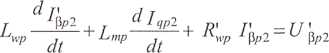
gdzie L_wp = L'_owp+L_lup.

Ze względu na sposób połączenia obwodów wirników możemy napisać:

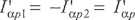
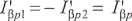
(8.2a)

(8.2b)