17

A.S. Jagiełło, Systemy elektromechaniczne dla elektryków

Ostatecznie więc pulsacja własna maszyny obcowzbudnej prądu stałego wyraża się wzorem:

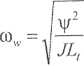
f d r₍ y

\2J 2L_t)

(4.7)

W obcowzbudnych maszynach komutatorowych prądu stałego średnich i dużych zwasze spełniona jest silna nierówność —((-7-. ^°żna zatem napisać:

J L_t

«_= i-Ł-

\JL,

R

2LJ

(4.8)

Jak wynika z relacji (4.7), pulsacja własna układu elektromechanicznego zależna jest od wielkości elektrycznych    oraz mechanicznych (J,D).

Rozważmy teraz pulsację rezonansową analizowanego tu układu elektromechanicznego. W tym celu przyjmiemy monoharmoniczny typ wymuszenia w równaniu macierzowym (4.5).

	[U ] ^ m i !
[T J

sin(coć)

(4.9)

Stosując rachunek symboliczny dla wyznaczenia rozwiązania asymptotycznego równania (4.5) z wymuszeniem (4.9), możemy napisać:

(4.10)

\R_t+jO)Lt \|/ TZl p⁷*.]

-¥    yco/jLaJ [T_m\

Zgodnie z zamieszczonymi powyżej wyjaśnieniami wyrażenie — zostało pominięte. Rozwiązanie tego równania ma postać:

(4.11)

j~ L\_1_-¥ 1X1

_LOj \|/² - co² JL_t f j(0R_tJ L \|/    R₍+ ju>L, JL T_m J

Wykonując zaznaczone działania i wracając do postaci czasowej, otrzymujemy wyrażenia na funkcją opisującą kształt prądu twomika:

V(V-co²y£,)²+((oĄy)³

sin(octf - a - p)

(4.12a)

gdzie

.    (ioJU_m)„    f co \

a = a tani-— i, P = a tani —-—-i

^r    i - -2    -2 TT !

t    ‘    vV“-0)Vi,j

oraz funkcję opisującą kształt pulsacji kątowej wirnika:

(4.12b)

_a (S^ESS_sm(„_łT-₈₎

y (\j/“ -<słJL_t j +(co7?,J^r)²

gdzie

y = a tanf—1

Wyznaczenie pulsacji rezonansowej sprowadza się do wyznaczenia ekstremum amplitud w wyrażeniach (4.12) jako funkcji pulsacji napięcia zasilającego. Postać tych amplitud wskazuje, że wyznaczenie ekstremum jest jednocześnie wyznaczeniem maksimum. Trzeba tu jednak zauważyć, że wartość pulsacji rezonansowej określanej dla prądu będzie inna od pulsacji rezonansowej określanej dla pulsacji kątowej wirnika.

Dla prądu twomika pulsację rezonansową określa relacja:

=

W,

( y7

JU

V

natomiast analogiczna wielkość dla pulsacji kątowej wirnika ma postać:

V W.

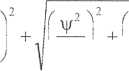
+ 2

{JLJ {L_tT_m Ljl JL_t {L,Tj h)T_n

(4.13b)

Cechą charakterystyczną tych pulsacji jest ich zależność nie tylko od parametrów sy.icmu, ale także od amplitud funkcji wymuszających. Jeśli jednak przyjąć, że jedno z okresowych wymuszeń jest niezerowe, niezależnie które, to pulsację