30

52 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków

^L<t	0	VF«,1.		,	* . \	r°	~Ld	^0 IM 1—
0	Ld	0 —: dt \	k	+M^1		\b	0	S^M-tr 1
W#	0	b j	kl			L^0	0	^0 Jb/J

\^Rs	0	o T^l	O 1___
! o	X,	ii V^2" o	! o
L°	0	^Rr}Jf\	W

d\}w i ’^T^=P<	^+ T»	(7.1 b)
S? |l5^’ ii i ^3	£MdfIfIq+Ts	(7.1 c)

Wielkości T_w i T_s są momentami działającymi po obu stronach sprzęgła.

Rozważmy obecnie charakterystykę statyczną takiego sprzęgła. Na jej podstawie można ocenić jego własności, a nade wszystko wartość przenoszonego momentu. Równania (7.1) przyjmą postać:

r o	~Ld	0	V	1	i o o	IV		roi
P{aw-Qs)Ld	0		k	+	0 Rs 0	^lq	-	0
L°	0	0	kJ	l	1 O o	ib.		k/J
	-p(nw-nX				0	v	f	Ol
P{aw-Qs)Ld	Rs		p{Qw-Qs)^Mdf			b	=	^0
0	0				Rf	M	'	Uf\

(7.2a)

4=^

(7.2c

(7.2b

4

Zatem moment przenoszony przez sprzęgło wyrazi się wzorem:

_T = _P{ri_M yKT

ⁱel P\S2^Mdf \ n „2 .    2(_n n V r²

\^Rf J ^Rs +P l&_W~^Qs) ^Ld

lub w postaci zbliżonej do wzoru Klossa:

2 _P(n_w-a,Y

Tel=P

\^Ld)

gdzie = f2_M, = const, -&_s = O._s= const

(7.3)

+_P²(ci_w-ci,f

Na podstawie wzoru (7.3) można określić maksymalny moment, którym można obciążyć sprzęgło:

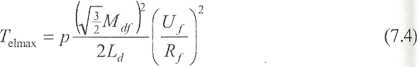
a także różnicę prędkości, przy której ów maksymalny moment występuje:

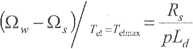
(7.5)

Jak wynika z wzoru (7.5), im dłuższa jest stała czasowa obwodu stojana, tym poślizg statyczny (różnica prędkości obu części sprzęgła) jest mniejszy. Natomiast maksymalny moment statyczny przenoszony przez sprzęgło zależny jest dla danego sprzęgła wyłącznie od kwadratu prądu magnesującego..