16

24 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków

24 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków

W yrażenie

£	JB_ V
M	U Aj

nazywamy pulsacją (częstością) własną układu

i oznaczamy co_M.. Przez pulsacją rezonansową rozumie się taką wartość pulsacji wymuszenia harmonicznego, przy której amplituda odpowiedzi asymptotycznej układu osiąga wartość maksymalną. Rozważmy zatem równanie (4.1), dla którego W - W_m sin(co^). Rozwiązanie asymptotyczne będzie miało postać:

x= ,- =sin(co^-cp)    (4.3)

( coB

gdzie (p = a tan -:— |.

\C~co~A j

Dla wyznaczenia pulsacji rezonansowej wystarczy teraz obliczyć pulsację, dla której amplituda funkcji danej relacją(4.3) osiąga maksimum. Wobec powyższego:

—)=0 + to ²B²

i,    K,

Po wykonaniu zaznaczonych działań otrzymuje się wyrażenie:

0)

rez

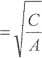
f B V

Ia/2

(4.4)

Jak łatwo spostrzec, pulsację rezonansowa i własna różnią się od siebie, jeśli lylko analizowany układ zawiera człon tłumiący B. Tak jest w przypadku układów jednorodnych, tj. wyłącznie mechanicznych (analizowane położenie) lub wyłącznie elektrycznych (analizowany ładunek). Zagadnienie znacznie się komplikuje w przypadku analizy nawet prostego układu elektromechanicznego. Rozważmy zatem równania modelu matematycznego silnika obcowzbudnego prądu stałego.

(4.5)

d\L,Olijp, _VJ,;1

dt\_ 0 /|aj - \\I    D}J1\

Powyższe równanie macierzowe możemy rozwiązać metodą przewidywania, analizując równanie jednorodne. I tak przewidujemy rozwiązanie w postaci:

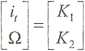
exp(rć)

Podstawiając przewidywane rozwiązanie do jednorodnej części równania (3.5), otrzymujemy:

lub

0

°T

rJ |

K, |    i

exp(rO +

^Kl\    .[

-¥

i

d\[k₂ J

exp(r/) =

~0~|

.oj

r ^rLi+^Rt

L

V T^il

r7 + DjU:₂]

exp(rO =

fo'

(4.6)

Rozwiązanie równania (4.6) będzie nietrywialne wtedy i tylko wtedy, gdy:

det!

\rL,+R,

L

¥

rJ + D

lub

JL,r² + {L,D + JR, + V|/² + R,D = 0

Rozwiązanie powyższego równania ma postać:

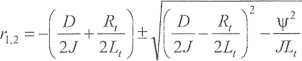
W związku z tym, że nasze rozważania ograniczają się tu do przebiegów oscylacyjnych, z możliwych tu rozwiązań wybieramy te, dla których r_{[ 2} są liczbami zespolonymi, zatem:

(^.₊a.)+ , (ZjZIaT

[2J 2LJ \JL_t [2 J 2 L_t)