25

42 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków

stąd dla zerowych warunków początkowych rozwiązanie będzie miało postać:

A« = -^-sin(c«) co"7_z

Z warunków zadania wynika, że Q(t,L) = $_z(t), zatem:

(

(OTk

tgj oo. —L Jsin(<a0 = -

co V

-sin(coO

W powyższej relacji będzie zachodziła równość funkcji sinusoidalnych, jeśli będą równe ich amplitudy. Mnożąc zatem obustronnie równanie przez co, otrzymujemy:

Z

(

J

,— tg! coJ—L ■Jjk { Vc

j

_ ^^ml 01/„

Oznaczając całkowity moment na swobodnym końcu analizowanego wału przez T_c, będzie on równy sumie momentów T_m + T_ml, zatem możemy napisać:

stąd

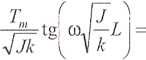
T_c~T_m

co/₂

Z_

o\J_z

T

ni

(OJ_z

)

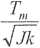
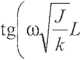
Z powyższej relacji można wyznaczyć wielkość momentu T_m:

Z,=-

^rr_cJJk

yflk - CO/_ztgf CoJZń

(5.15)

Podstawiając wyrażenie (5.15) do wzoru (5.7), otrzymamy ostateczne wyrażenie na kąt skręcenia wału:

( rr > rp • J Tc smj J—x [\/c ,		jsin(coO 1
OhJjk	yflk - COJ jgfcoJ V ^V	^k ).	( cos! CO^j	Z

(5.16)

W celu wyznaczenia pulsacji własnych tego układu należy przyrównać mianownik wyrażenia danego wzorem (5.16) do zera. W tym przypadku powoduje to ujawnienie się dodatkowych miejsc zerowych:

f ij

*fjk — COyv/_ztgl (Oy^jjL

lub

yfJk ;

00 jJ_z

(

tg! C0_;

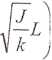
(5.17)

Zagadnienie rozwiązania równania (5.17) ze względu na zmienną C0ynajlepiej zilustrować rysunkiem.

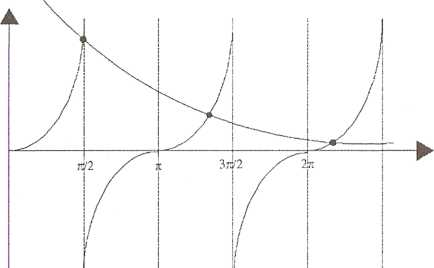
Rys. 12. Graficzna ilustracja rozwiązania równania (5.17)

Należy w tym miejscu przypomnieć, że wał mechaniczny analizowany jako układ ciągły ma nieskończenie wiele przeliczalnych pulsacji własnych (5.8). Jeśli jego swobodny koniec jest jeszcze wyposażony w element o innym, dodatkowym momencie bezwładności, to układ taki nie zmienia podstawowego, wcześniej wyznaczonego widma pulsacji, a jedynie ujawnia inne, dodatkowe widmo - i nieskończone, i przeliczalne, jak to wynika z rysunku 12.