23

38 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków

Zauważmy, że:

( e^ya + e~-'^a Y

l ² J

cos³ a

Jeśli odpowiednio pogrupujemy wyrażenia, otrzymamy: cos^{3 a} - “ [cos(3a) + 3 cos a]

Zatem wyznacznik dany wyrażeniem (5.10) można zapisać:

i^(4 cos³ a-3cosa)=cos(3a) = 0

stąd a =—(2/i-l), dla n = 1,2, 3...

6

Wykorzystując dokonane wyżej podstawienie, można napisać:

7t(2«-l)

cos—---

6

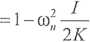
Powyższa relacja pozwala na otrzymanie wyrażenia na pulsacje własne układu z rysunku 4:

co.. =

2 K I

1 - cos

71(2/1-1)

lub

C0„

71(2/2-1)

12

(5.11)

Jak łatwo zauważyć, analizowany układ ma trzy pulsacje własne dla n równego 1, 2 i 3. Dla kolejnych wartości liczby naturalnej n wartości pulsacji albo będą się powtarzały, albo będą-jako ujemne - nierealizowalne fizycznie.

Aby opisać wał ciągły układem inercyjno-sprężystym, należy rozpatrzyć układ analogiczny jak na rysunku 3, tyle tylko, że złożony z dowolnej, skończonej liczby elementów [2]. Dokonamy tego, wykorzystując wnioski wynikające z powyżej przeprowadzonej analizy układu inercyjno-sprężystego złożonego z trzech bezwładności i trzech sprężystości.

Jc-śll uważnie przeanalizujemy postać macierzy sztywności dynamicznej danej relacją (5.9), to zauważymy, że jest to macierz o szczególnej budowie. Ze względu na to, że każdy krążek oddziałuje jedynie z sąsiednimi, z wyjątkiem pierwszego i ostatniego, zatem każdy jej wiersz zawiera tylko trzy niezerowe elementy. Natomiast wiersze pierwszy i ostatni zawierają jedynie po dwa niezerowe elementy. Wobec powyższego macierz sztywności dynamicznej Z będzie macierzą trójprze-kątną o postaci:

Z = K

	-i	0	—>	—>		—>	-> 0
K
-1	2-co^2 —	-i	0		—>	->	-> 0
	K
0	-1	2-co^2 —	0		->	->	-» 0
		K
0	0	-1					4
4	4	0					4
4	4	4					4
4	4	4					0
4	4	4					-i
0	0	0		->	—>	0	-1 1 — co^2 -

(5.12)

I

2 K

W celu wyznaczenia pulsacji własnych tego układu należy obliczyć wyznacznik z macierzy sztywności dynamicznej i przyrównać go do zera. Dlatego też, podob-

nie jak poprzednio, zastosujemy podstawienie: 1 - co'⁴ -¹— = cos a. Wtedy wyznacz-

2 K

.2 /

nik przyjmuje wartość [2] det(Z) = cos(ra), gdzie r jest rzędem macierzy Z. W tym przypadku rząd macierzy jest równy liczbie elementów, na które został podzielony analizowany wał. Po przyrównaniu do zera tego wyznacznika, czyli cos(roc) = 0 mamy:,

ot... =•

71(2/2-1)

2 r

/.i (cm

1 2 ¹ 1 — co... -= cosi

[71(2/2-1)

2 K