14

Ml A S Jagiełło, Systemy elektromechaniczne diet elektryków

• ,lt»4ll myjąć, źe elementy a_(j macierzy A są stałe, to powyższe równanie w /wni tym ujęciu macierzowym można napisać:

_Adq ₊ dB_ _{+ K} qt _{= w}    (₃.₅)

dt dt

gdzie W jest kolumnową macierzą wymuszeń.

W zdecydowanie większej ilości przypadków systemy elektromechaniczne składają się z elementów wykonujących ruch obrotowy. Z kolei, poza szczególnymi przypadkami, wirujące części maszyn są wyważone, stąd na obecnym etapie rozważań przyjmiemy, że macierz G jest tożsamościowo równa zeru. Jeśli ograniczyć jeszcze nasze rozważania do układów pozbawionych remanencji (magnetyzmu szczątkowego), to macierzowe równanie (3.5) przyjmie postać:

A—+ Kr/ = W

dt

Dla wyznaczenia macierzy sztywności dynamicznej przyjmijmy macierz wymuszeń w postaci:

W = W_/H sin(coć) - D<ż ostatecznie więc równanie powyższe przyjmie postać:

A-^4 + D^ + K? = W„, sin(oM)    (3.6)

dr dt

Poszukując rozwiązania asymptotycznego powyższego równania macierzowego, zastosujemy rachunek symboliczny. Możemy wtedy napisać:

(k - O)² A + y'coD)Q = W

stąd

Q =[k-co²A + ycoD^W    (3.7)

Macierz [k-co²A+ /'cod] ^_I w literaturze przedmiotu [2] oznaczana jest przez /, i nazywana „zespoloną macierzą sztywności dynamicznej”. Macierz do niej odwrotna nosi nazwę „zespolonej macierzy podatności dynamicznej”. I)l;i przypadków układów, dla których można pominąć straty, macierze te noszą nazwy, odpowiednio: „macierz sztywności dynamicznej” i „macierz podatności dynamicznej”.

Przykład

Rozważmy układ jak na rysunku 4:

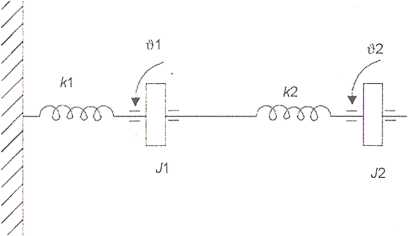
Rys. 4. Przykładowy układ mechaniczny sprężysto-bezwładnościowy Funkcja Lagrange’a dla tego układu ma postać:

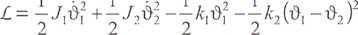
Wykorzystując równania Lagrange’a drugiego rodzaju (2.3), otrzymujemy:

d²A    _n d$.

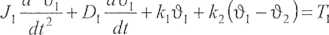
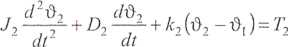
lub w zapisie macierzowym: