28

48 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków

Teraz wyrażenie (6.5) wynikające z drugiego warunku brzegowego przyjmie postać:

Im{(C,. + jC_lt)*(a- y'p)*[cos(©/) + ysin(a>0]*[cos(ocL)cos/2(pT)-ł-./sin(aL)sm/7(pZ,)]} T

= —sin(co t)

Po wykonaniu zaznaczonych działań otrzymujemy:

(- PC,. + aC_u )[cos(otL)cos /z((3Z,)cos(co/^t) - sin(al)sin/2((3L)sin(coO]+

T

+ (aC_r+|5C„ )[cos(ocL)cos ń(pZ,)sin(coO + sin(ocZ,)sin /?((3Z,)cos(co/)] =    sin(co/)

k

Aby mogła zachodzić powyższa równość w każdej chwili czasowej t, musi być spełniony następujący układ równań, w których niewiadomymi są C_r i C_u\

(- pC,. + aC_u )cos(aZ,)cosń(pZ,)+(aC_r + pC_M )sin(ań)sin h($L) = 0

(pC_r -aC_ł()sin(ocL)sin/2(pl)+(aC_/. +pC,₍)cos(ocZ)cos/7(pl) = -p-

k

Rozwiązując ten układ równań, otrzymujemy:

(6.10a)

(6.1 Ob)

^ _ T_m a cos(ocŁ)cos ń(pz,)+ Psin(aZ>)sin/2(pX) *    (a² +p²fcos²(aL)+sin/z²(pl)]

^ _ T_m Pcos(aL)cos/z(pZ,)-asin(aL)sinń(pZ-) ^    (a²+p²|cos²(ocZ,) + sin/2²(pZ)]

Wracając do poszukiwanego rozwiązania równania różniczkowego cząstkowego, możemy napisać:

© = Im {[(C_r + jC_u )*(cos co/ + jsin co/)] * [sin(ocx)cos ń(px)- jcos(ocr) sin /i(px)] }

Po wykonaniu zaznaczonych działań otrzymujemy:

0 = C_r [sin(ooc) cos/z(px)sin(co/)-cos(ocx:)sin A(px)cos(coO]+

-C_H[cos(ocx)sin/2(Px)sin(co/) + sin(ocx)cosń(Px)cos(co/)]    (6.11)

lub w zapisie zwartym:

6 = SZ 2

gdzie

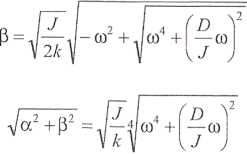
[e^p* cos(co/ - ax + y) - e cos(co/ + coc + y)]    (6.12)

_    | pcos(aZ,)cos/?((3z)+asin(aL)sin/7(pz) j

^    L P sin(a£)sin /z((3Z) + occos(ol£,)cos A(pl) J

a ponieważ

V^Cr+C«

2    2* ^_a² +p²-y/^c°s²(otZ,)+sin/»²(pz,)

zatem poszukiwane wyrażenie na kąt skręcenia wału przyjmie postać:

q _ ^T,n ^gP'^v cos(o)^ - coc + y)- e ** cos(cot + ax + y) ^ yja² +[3²i/cos²(al)+sinA²(pZ)

gdzie

(6-13)

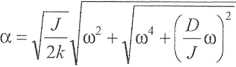
natomiast

Na podstawie wyrażenia (6.13) możemy stwierdzić, że wzdłuż wału rozchodzą się dwie przeciwbieżne fale o równej co do wartości prędkości:

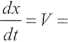
(6.14)