11

A.S. Jagiełło, Systemy elektromechaniczne dla elektryków

Relacja (2.2) pozwala napisać wyrażenie na koenergię kinetyczną układów mechanicznych:

S

5

^eko = 'LPj^j - Z \Vjdpi = Z_PjdVj

(2.16)

W przypadku gdy pęd jest proporcjonalny do prędkości, wyrażenie (2.16) przyjmuje postać:

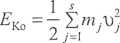
(2.17)

Łatwo teraz zauważyć, że dla układów liniowych (my = const) koenergia kinetyczna jest równa energii kinetycznej. Fakt ten można zilustrować graficznie w przypadku układu jednowymiarowego, tj. gdy j = 1 (patrz rys. 1).

W układach elektromechanicznych, dla przypadku ruchu obrotowego, zazwyczaj mamy do czynienia z sytuacją, w której kierunek wektora momentu pędu pokrywa się z osią obrotu wirujących mas. Wobec powyższego wyrażenie na ko-cncrgię kinetyczną mas wirujących można zapisać w postaci:

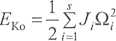
(2.18)

gdzie:

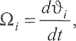
£,• - kąt obrotu i-tej masy wirującej,

J_i - moment bezwładności i-tej masy wirującej.

p

A

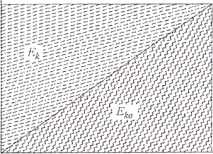
Rys. 1. Graficzna interpretacja energii i koenergii kinetycznej dla układu liniowego jednowymiarowego

v

Przechodząc do pola elektromagnetycznego, ogólne wyrażenie na energią ma tu postać:

E=t\U;dq,(2.19)

/“I

gdzie:

Uj - z-te napięcie w obwodzie,

- z-ty ładunek obwodu.

Jeśli napięcie jest wynikiem zmian pola magnetycznego obejmowanego przez obwód elektryczny, to zgodnie z prawem Faradaya mamy:

'    dt

W powyższym równaniu zachodzi słaba nierówność s>r. Podstawiając wyrażenie (2.20) do wzoru (2.19), otrzymujemy:

dt

II

Wykorzystując wprowadzone pojęcie koenergii kinetycznej, możemy napisać:

^Kopm = II^ tól > ?2> -• • Ar ) ^d4i    (2-22)

/=I

Jeśli natomiast napięcie jest wynikiem określonego rozłożenia ładunków elektrycznych w przestrzeni, to najczęściej mamy do czynienia z sytuacją w której relacja między napięciem a ładunkiem całkowitym ma postać:

(2.23)

gdzie C_i jest z-tą pojemnością w analizowanym układzie. Po podstawieniu relacji (2.23) do wzoru (2.19), otrzymujemy wyrażenie na energię pola elektrycznego:

Ą. = tf Cfi,dq,    (2.24)

.* /=!

Porównując wyrażenia na energię zawartą w polu elektrycznym z energią potencjalną oraz koenergię zawartą w polu elektromagnetycznym z koenergią kinetyczną zauważamy podobieństwo strukturalne. Możemy zatem, dla potrzeb równań Lagrange’a, energię zawartą w polu elektrycznym traktować jako energię potencjalną natomiast energię zawartą w polu elektromagnetycznym jako koenergią kinetyczną.