21
34 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków
przy warunkach brzegowych:
©0,0) = 0 (5.3a)
*|r| =r„sin(cor) (5.3b)
ĆX 'X=L
W celu rozwiązania tego równania zastosujemy metodę rozdzielenia zmiennych Fouriera. W metodzie tej zakłada się, że rozwiązanie będące funkcją dwóch zmiennych t i x [0(ć,x)j można przedstawić w postaci iloczynu dwóch funkcji, z których każda jest funkcją tylko jednej zmiennej, i tak:
Q(x,t) = X(x)*T(t) (5.4)
Po podstawieniu powyższego wyrażenia do równania (5.2) otrzymujemy:
JX(x)Tn (t) = kX" (.x)T{t)
gdzie oznaczono przez 7’" =
oraz przez X"{x)
d2X{x) dx2
Po podzieleniu stronami możemy napisać:
X”(x) __ J T"{t) X(x) k T{t)
Dodając do równania zero w postaci A,2 - A2, otrzymujemy:
X"
X
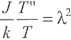
-A2
Teraz, rozdzielając zmienne, uzyskujemy dwa niezależne równania różniczkowe:
A2
X11
o rozwiązaniu:
X(t) = Cj sin h(kx) + C2 cos h(hc)
oraz
T" k
= -V
T J
lub
= X.
£
o rozwiązaniu:
T(t) = C3sin J—Xt 1 V J
+ C4C0S
Zgodnie zatem z relacją(5.4) napiszemy:
0(ć,x) = [C, sin h(Xx) + C2 cos/z(Aa')]
C, sin
+ C4 cos
K -J
(5.5)
Z warunku brzegowego (5.3a) wynika zerowa wartość stałej C2. Teraz rozwiązanie równania (5.5) przyjmie postać:
Q(ć,x) = i^CjC3 sin
j
+ CjC4 cos|
sin h(Xx) (5.6
W celu wyznaczenia stałych rozwiązania (5.6) wykorzystamy drugi warunel brzegowy (5.3b):
kX
C,C3 sin
X^~^t) + CjC4 cos(xJ~^t
cos h(XL) = Tm sin(coO
stąd
C,C4= 0
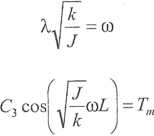
Wyszukiwarka
Podobne podstrony:
42 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków stąd dla zerowych warunków początkowych
126 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków Współczynnik przenoszenia p dla
48 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków Teraz wyrażenie (6.5) wynikające z drugi
A.S. Jagiełło, Systemy elektromechaniczne dla elektryków Relacja (2.2) pozwala napisać wyrażenie na
U) A,S. Jagiełło, Systemy elektromechaniczne dla elektryków Wielkości W i stanowią ogólny zapis sił
IX A S Jagiełło, Systemy elektromechaniczne dla elektryków Przebieg strat na styku koło-szyna przeds
22 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków Dla wyznaczenia macierzy sztywności
24 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków 24 A.S. Jagiełło, Systemy elektromechani
A.S. Jagiełło, Systemy elektromechaniczne dla elektryków Ostatecznie więc pulsacja własna maszyny
28 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków dla obydwu zmiennych stają się niezależn
30 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków Rys. 7. Charakterystyka rezonansowa siln
38 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków Zauważmy, że: ( eya + e~- a Y l 2 J cos3
40 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków stąd 71(2/2-1) 4 r (5.13) Aby sprawdzić,
52 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków L<t 0 VF«,1. , * .
58 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków VI
66 A.S. Jagiełło, Systemy elektromechaniczne dla elektrykówNa rysunku 18, w kolejności od dołu, zazn
70 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków 70 A.S. Jagiełło, Systemy elektromechani
więcej podobnych podstron