12

U) A,S. Jagiełło, Systemy elektromechaniczne dla elektryków

Wielkości W i stanowią ogólny zapis sił (wymuszeń), mających swoje źródło w innego typu energiach. Pośród nich na szczególną uwagę zasługują siły (wymuszenia) dyssypatywne. W układach elektrycznych są to spadki napięć określane relacją:

U_i=R_lq_i    (2.25)

gdzie Rj jest/-tą rezystancją obwodu elektrycznego.

W układach mechanicznych problem jest o tyle bardziej skomplikowany, że straty sił (momentów) mogą mieć wiele różnych przyczyn, np. tarcie „suche”, wi-skotyczne - przy ruchu laminamym, turbulentnym, czy tarcie „potoczyste”. Najczęściej dla przypadków analizy prostych układów liniowych przyjmuje się relację analogiczną do spadku napięcia na rezystancji, zatem:

T_i=D_iq_i    (2.26)

gdzie A-jest współczynnikiem dyssypacji układu mechanicznego.

Dla tarcia „suchego” odpowiednią relację możemy zapisać w postaci:

sign(<7,.)    (2.27)

gdzie:

Nj - /-ta siła nacisku prostopadła do trących powierzchni, fi,- - /-ty współczynnik tarcia „suchego”.

Szczególnym rodzajem strat wywołanych tarciem jest tarcie związane z toczeniem się koła po płaskiej powierzchni, niekiedy nazywane tarciem potoczystym. W naszych rozważaniach zajmiemy się tarciem toczącego się koła stalowego po stalowej szynie. Jest to problem najczęściej analizowany w trakcji elektrycznej. Powszechnie wiadomo, że podczas toczenia się koła po szynie, w warunkach pokonywania oporów ruchu, droga wynikająca z obwodu koła jest większa od drogi rzeczywiście przebytej przez to koło. Zjawisko to nosi nazwę poślizgu i wyrażamy je wzorem:

Qr-V

s =-

Qr

gdzie D. jest prędkością kątową koła, r jego promieniem, natomiast V prędkością liniową osi jego obrotu. Siła styczna działająca na styku koło-szyna określana jest wzorem [6].

F =

20if s_bs

I 2    2

71 ^+J²

-l- a tan;

fs))

UJJ

(2.28)

gdzie

^b 2Cna²b

W powyższych wzorach przez Q oznaczono siłę nacisku koła na szynę, fi współczynnik tarcia zależny od prędkości, przy czym przez p,₀ - współczyni maksymalny, natomiast ,11^ - graniczny. Wielkości C, a, b są stałymi związany z powierzchnią styku koło-szyna. Zależność tej siły F od poślizgu przedstawić na rysunku 2.

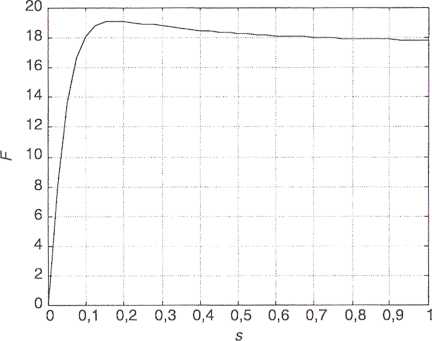
Rys. 2. Przykładowy przebieg siły przyczepności w funkcji poślizgu

Jeśli przyjąć, że koło jest napędzane momentem T_nap, to straty mocy, jakie pi wstają w obszarze tego styku można wyrazić wzorem:

AP = T^a - FV = nh -    N^+a tany i(l - 5)}    (2.2<

V.    C b    J    j

gdzie orzez W oznaczono liczbę kół umieszczonych na jednej osi, napędzanych tyi siiinvm morpgntem napędowym. W układach trakcyjnych najczęściej N= 2.