mech2 153

304

F

Zauważymy, że otrzymana wartość x Jest równa promieniowi bezwładności pręta AB względem osi przechodzącej przez środek ciężkości

Maksymalna' prędkość kątowa

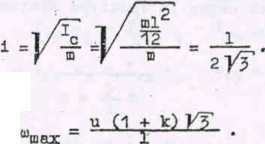
Zadanie 18 (rys. 224)

m ^	A B
	0
2m —.	C

Dwa jednorodne pręty AB i BG o długościach 1, 21 i‘ masach m i 2m znajdują się w spoczynku w położeniu pionowym. Pręt AB jest osadzony przegubowo w punkcie A, pręt BC zaś jest połączony z prętem AB przegubowo. W pewnej chwili do środka O pręta BC przyłożono impuls S, skierowany prostopadle do osi pręta. Obliczyć prędkości kątowe ui/j i tog obu prętów w pierwszej chwili po uderzeniu oraz prędkośoi środków ciężkości prętów V* i Vp w tej obwili.

Odp. <4, =    £ ,

^{11)2 =} & ET •

•§■ »

^v2 = ^ *T *

Kys. 224

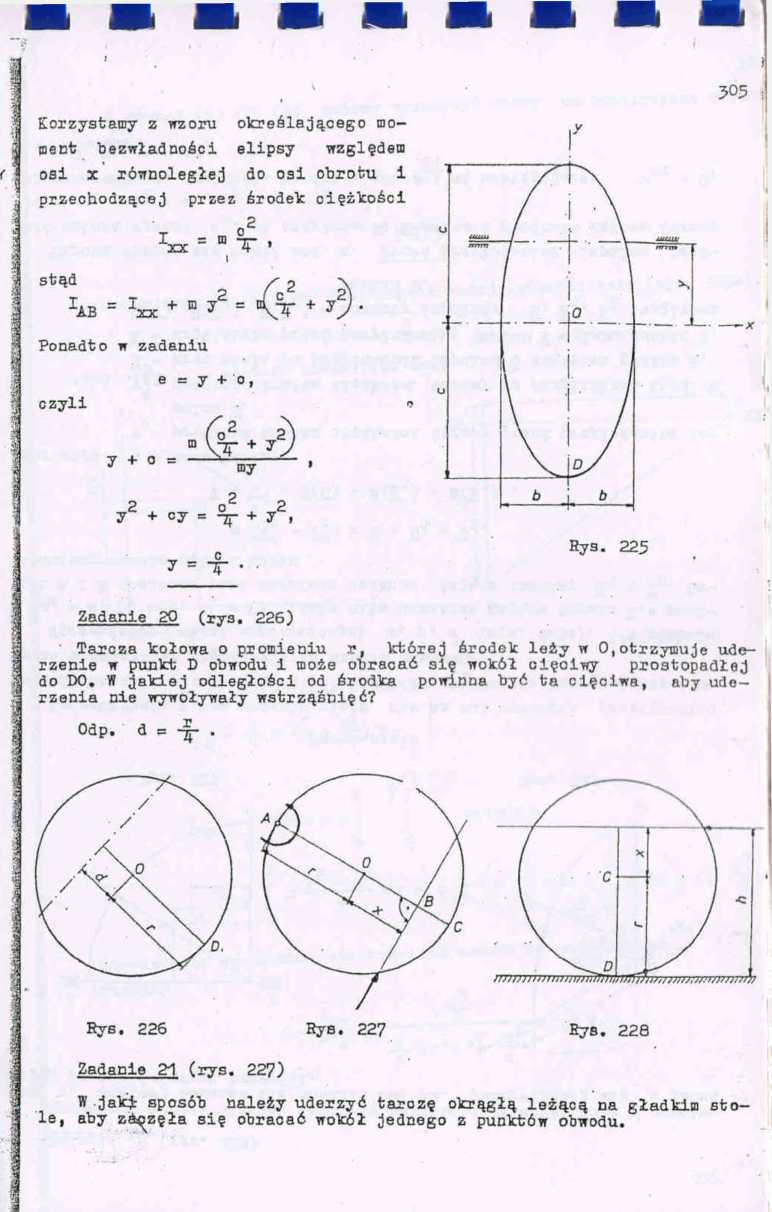
Zadanie 19 (rys. 225)

Tarcza w kształcie elipsy o półosiach b i c oraz masie m, może obracać się dookoła osi AB. Obliozyć, jaka powinna być odległość y osi AB od środka tarczy O aby uderzenia,skierowane prostopadle do tarczy w punkcie D, nie wywoływały dodatkowych reakcji osi obrotu.

Rozwiązanie

Jest to przypadek uderzeń mimośrodowych. Aby nie wystąpiły dodatkowe reakcje w łożyskach osi obrotu, oś obrotu musi znaleźć się w takim położeniu, aby punkt D był środkiem uderzeń ciała, obraoającego się wokół osi AB. Dla ciał, mających płaszczyznę symetrii przechodzącą przez środek ciężkości 1 prostopadłą do osi obrotu, odległość środka uderzeń od osi obrotu wyraża się wzorem:

UTcT •

w którym ^IAB — moment bezwładności ciała względem osi obrotu, d odległość środka ciężkośoi ciała od ob! obrotu.