mech2 164

r

326

u₂ - długość części Bznura między ciężarem G₂ i blokiem 0₂,

stąd

5y^ = sin a 6 u^,

i

6 y₂ = sinp 6 u₂-

Równanie więzów

+ 2y + u₂ = const,

stąd

⁶ 7 = ^+5u2) *

Wstawiając wyznaczone zależności do równania prac przygotowanych otrzymamy;

G^sinaS u^ +• G₂sin P5 u₂ - G    + 6u^) = 0,

i

(G^slna G) ó + (^G^sinP —— G) 6u₂ = 0.

Ze względu na to, że przyrosty 6U^ i fiUg są od siebie niezależne, muszą być spełnione równania:

i

G^sina - — G = 0,

G₂3in p - -y 0 = 0, •

stąd

G = -——

1    2 sin a '

_r __G_

*2 “ 2 sin P •*

Zadanie 9 (rys. 242)

Na końcach nlerozciągliwej liny zawieszono dwa ciężary P i Q.Linę przerzucono przez dwa Btałe gładkie krążki A i B.Ciężar P leży na gładkiej równi pochyłej tworzącej kąt a z poziomem.. Między krążkami A i B zawieszono dodatkowy krążek C z zamocowanym ciężarem 5.. Mając dany ciężar P znaleźć wartości ciężarów G i Q w położeniu równowagi.

Odp. G = 2P sin a ,

Q = P sin cc.

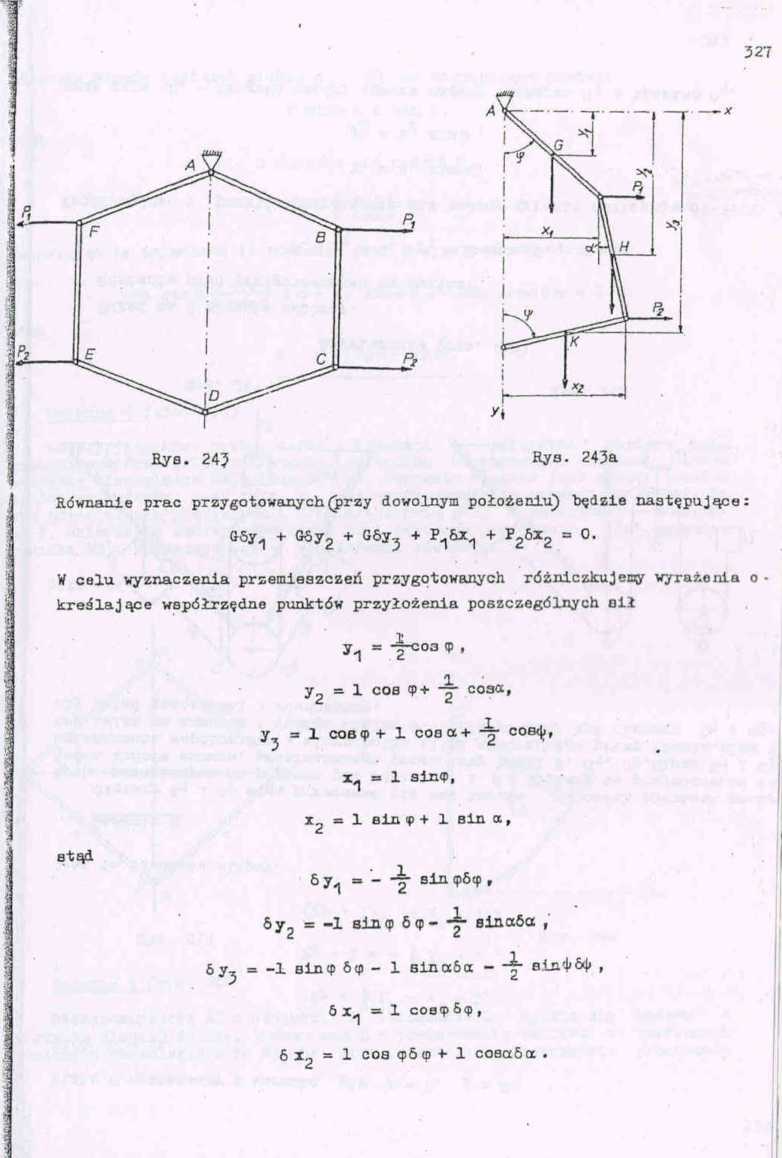
Zadanie 10 (rys. 243)

Sześciobok ABCDEP, składający się z sześciu równych połączonych przegubami prętów o ciężarze Q i .długości 1, zawieszono w wierzchołku A.W~wierzchołkach B,C,S i F przyłożono siły P-i 1 P₂ jak na rys. 243. Znaleźć przy Jakich wartościach sił Pą i P₂ sześciobok będzie foremny.

Rozwiązanie

Jest to układ o dwóch stopniach swobody.

Ze względu na symetrię rozpatrywać będziemy tylko połowę układu (rys, 243a).    ^V

[i

i

1

_J _