mech2 43

li I

f i

S^ł

= ~a_ud - a_w • cos 60° = -9 - 355 * 0,5 = -186 cm/s^,

a_z = —cos 30° = -355 '    = -308 cm/s¹,

a = 1/a^ + e¹ + a¹ = 395 cm/s¹.

Wyniki rozwiązania zestawiono w tabeli 20.

Tabela 20

UJ u e-^2	Prędkość, cm/s			"u s-^1
	^vu	^?w	V
-0,93	9,3	65,2	65,9	-10,2

Przyspieszenie, cm/s*

*ud	*uo	WD		^aC	3^	*7	^az	a
9	102	0	-355	61	165	-186	-308	395

B. Złożony ruch ciała sztywnego (składanie obrotów wokół osi równoległych i przeginających się) 3.3. Określenie prędkości kątowych członów przekładni planetarnej

z kołami walcowymi

Zadanie K-13

Określić prędkości kątowe wału biernego II i satelitów reduktora prędkości.

Schematy reduktorów zestawiono na rys. 54-56, a odpowiednie daDe * tabeli 21.

Przykład rozwiązania zadania

Dane wyjściowe: schemat reduktora (rys. 57)i promienie kół: r^ = }0, *2 - 151 1* = 30, r^ = 73 cm,• obroty nj = 800 obr/min, n^ = 200 obr/cin.

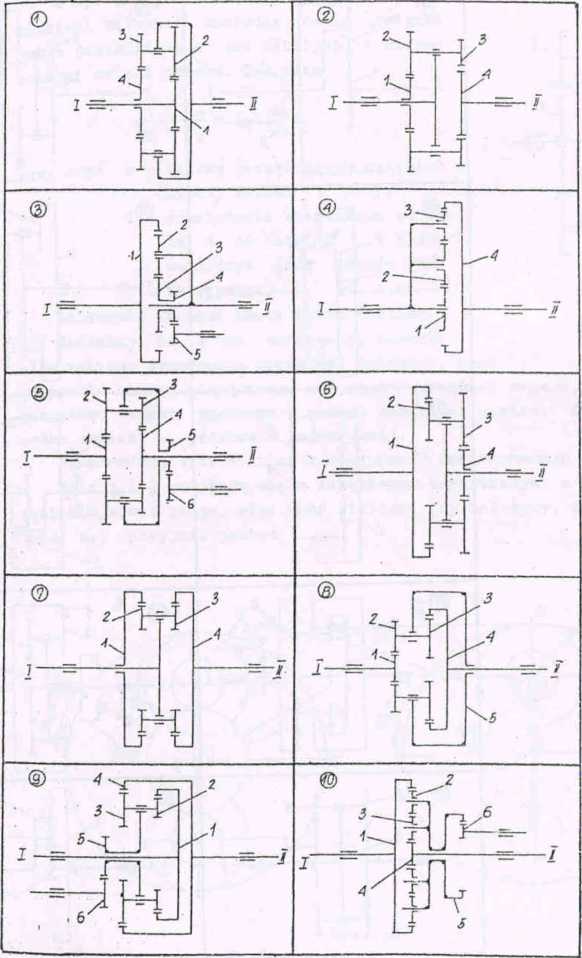
Rys. 54

1

Ketoda WilliBa polega na rozpatrywaniu ruchu elementów przekładni względrm jarztua. Metoda ta umożliwia określanie prędkości kątowych członów mej paniztou uczestniczących w dwóch obrotach: unoszenia i względnya. Soła reduktora uczestniczą? a) we względnym obrocie (w odniesieniu do

2

Rozwiązanie zadania sposobem Willisa