mech2 73

u

■m

stąd

0 V_r

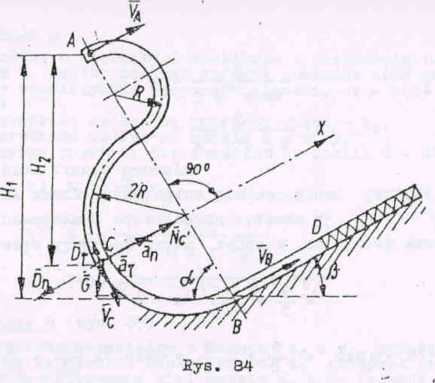
N_c = G cos 60° + D_q =; wg oos 60° + -~ =

Y²    2

=i n (g cos 60° +'^|) = 0,5(9,81-0,5 +    = 25,2 N.

Poszukiwana ciśnienia Nę kulki na ściankę rurki Jest równe modułowi zn. lazionej reakcji Nq ale skierowane w przeciwną stronę.

Prędkość kulki w położeniu D obliczymy ^stosując na odcinku BD zasat równoważności pędu i impulsu (ry3. 85):

® ^vDx “ " ^VBx = V

"I

145

jj/j punktu materialnego są przyłożone: siła ciężkości S, reakcja ścianki jpurki i siła tarcia |F| = f K* = f G cos p .

Jeżeli    ,    • .

^TDx=^vD’ ^T-=^Vt

"Bx “ B¹

= -G sinp • t - F t = -mg sin p • t - f mg cos p • t ,

fco zasada równoważności pędu i impulsu na odcinku BD przyjmie postać m v_Q - m t_b = -mg sinp • t - t mg cosp • t,

skąd

r = Vfi - gt(sinp + f cosp) = 4,59 - 9,81-0,1(0,5 + 0,1-0,856) =4,0^ m/s.

po obliczenia wartości maksymalnego ściśnięcia h sprężyny na odcinku pa skorzystamy z zasady równoważności pracy i energii kinetycznej (rys.

b_t

przy czym

^JB “ ^BD “ ^D-E'

•    2 p • •

^I*D—S = “ ^£2^~ “ ŚH3 “ F Ł.

Uwzględniająo, że v_B = O i E~ = b- sin (B, otrzymujemy:

2    m

2-£- + G(sin p+ f cosp) h--i 0

lub

_h2 ₊ 2G(slnP + f cos p) _b _ ^{m V}D _{= Q<}

Bozwiązując otrzymane równanie względem h otrzymujemy:

_b _ _ G(sin P+ f cos _|~|^/^G(sin P + f coa8)j ₊

₌ _ 0,$-9,81 (0^_ t Pj.1_*Q,866). _±

_±y[p^-9.^B-tC°.?_u5o°.VQ,BB6^ , 0^    -

m v_r

01'

= -0,005 ± 0,090 m.

Przyjmując w szukanej wielkości wartość dodatnią mamy

h = -0,005 + 0,090 = 0,08? m.

■