mech2 68

134

Rozwiązanie

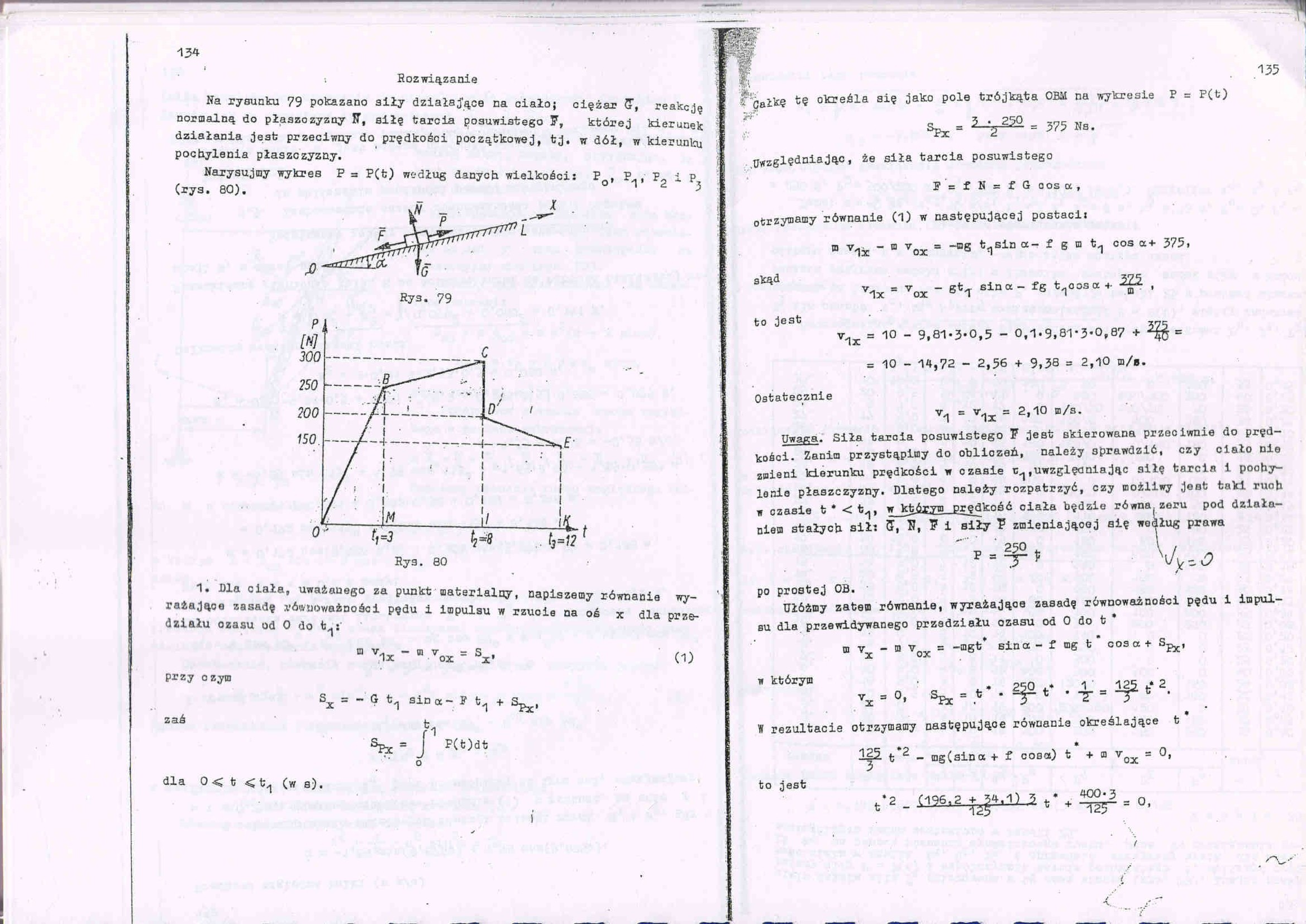
Na rysunku 79 pokazano siły działające na ciało; ciężar C, reakcję normalną do płaszozyzny IT, siłę tarcia posuwistego F, której kierunek działania jest przeciwny do prędkości początkowej, tj. w dół, w kierunku pochylenia płaszczyzny.

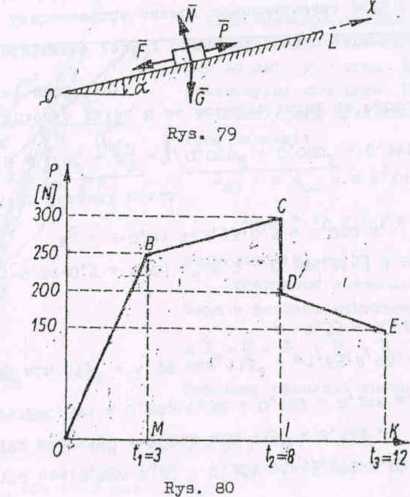
Narysujmy wykres P = P(t) według danych wielkości: P_Q,    i p

(rys. 80).

1. Dla ciała, uważanego za punkt materialny, napiszemy równanie wy-rażająoe zasadę równoważności pędu i impulsu w rzuoie na oś x dla przedziału ozasu od O do t^j'

" ^v1x - “ ^rox = ^BX'    (1)

przy ozym

S_x = - G t^ sina - F t^ + Sp^,

²³⁴    fi

%

j P(t)dt

O

dla O < t < t^ (w s).

w

■»

■: p

135

i ’_Ca>kę tę określa się jako pole trójkąta OBM na 'wykresie P = P(t) ? '    Sftc - ^ŁV⁵² * 5” Ha.

Uwzględniając, że siła tarcia posuwistego

P = fN=fGoosa,

otrzymamy równanie (1) w następującej postaci:

n v_1x - m v_QX = -mg t^sin a- f g b t₁ cos a+ 375,

^v1x ^{= v}ox “ ^6tT ^sina~ ^f6 t_noosa+    ,

skąd to jest

'1x

= 10 - 9,81.3*0,5 - 0,1.9,81*3*0,87 + ■ = 10 - 14,72 - 2,56 + 9,3Q = 2,10 dj/b.

Ostatecznie

= v_1x = 2,10 m/s.

Uwaga. Siła tarcia posuwistego F jest skierowana przeciwnie do prędkości. Zanim przystąpimy do obliczeń, należy sprawdzić, czy ciało nie zmieni kierunku prędkości w czasie ^.uwzględniając siłę tarcia i poohy^ lenie płaszczyzny. Dlatego należy rozpatrzyć, czy możliwy jest taki ruob w czasie t * < t^, w którym prędkość oiała będzie równa.zeru pod działaniem stałych sił: 5, U, F i siły F zmieniającej się według prawa

\

iK-.o

po prostej OB.

Ułóżmy zatem równanie, wyrażające zasadę równoważności pędu i impulsu dla przewidywanego przedziału ozasu od O do t *

m v - m v = -mgt sina - f mg t cos a + S-, ,

w którym

n a *. •    250 .♦    1    12£ x* 2

= °»    = t . -5r * * t - ~r ^fc •

W rezultacie otrzymamy następujące równanie określające t 125 x/2

t ^ - mg(sina + f cosas) t + m v_ox = 0,

to jest

t*2 - (196,2 ^,11 2 _t* ₊

400*3

125

= O,

'"V-