mechanika116

a_M(i) = a_k ♦ a_w * a_c ~ a” -a_w+ a_c = — ubu_x cos w,/

.v>

* 2 2 . ' - —- bu>, sin ió.t

l fi

- — w²&(l - sino>,r) + —doł^sinwj/

fi    fi

Obliczenia odpowiadające chwili /, = 3it/(2ojj):

. 3it .    .    3* _n

sin o, r, = sin— = -1, cosn>, f, * cos-— = 0

s(t) ~ b (-l) = -b —► punkt materialny jest w' położeniu A

v_w(f,) - bu)_xO * 0

«*(*!> = -bu]-(-1) = bu]

r(t_x) = ^[1 - <-!)] = 2b

v_M(r.) = —^*>(1 -{-l))e_x = -~ube_t V5

^('i) "    -(-l>] + -p^«J(-¹)ló_ł =

y5    1/5    V⁵    I

= —    + —(-2u²b - u]b)e

fi ⁷ fi

Zadanie rozwiązano przy założeniu, że położ.enie tarczy jest jednakowi w chwili bieżącej t i w chwili

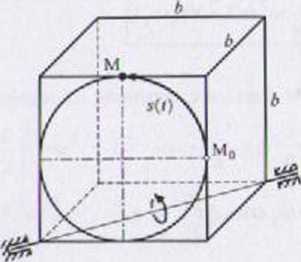
Zadanie 2.36

Sześcian o boku b obraca się jednostajni# I z prędkością kątową cj, wokół przek.|ln»'| ściany dolnej. Punkt materialny M porwali I się po okręgu wpisanym w ścianę boc/iui, ruchem jednostajnie    przyspieszonym

z przyspieszeniem stycznym a,. Wy/iw cz.yć prędkość i przyspieszenie punktu M w chwilowej konfiguracji układu. W cl»v\|i li początkowej prędkość względna )• 4 równa 0.

Dane: b = 0,4 m. w = 10 rad/s, a, = 2 mfs⁷

232

Rozwiązanie

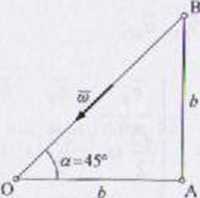
i Punkt M jest w ruchu złożonym. Ruch unoszeniu jest obrotowy jednostajny, ■•okół przekątnej ściany dolnej. Ruch względny jest po okręgu o promieniu bf2, •ostajnie przyspieszony. Początek układu xyz należy przyjąć na osi obrotu Sianu. Ze względu na ukośne położenie wektora u, obliczenia iloczynów sektorowych wykonujemy z wykorzystaniem zapisu wyznacznikowego.

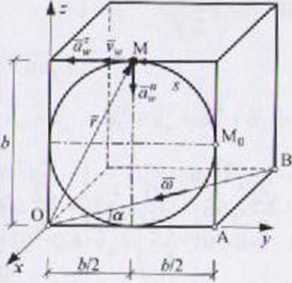
>1 iczenia wstępne:

In <i cos a = — 2

- fi - fi -

u sin c ■ c ^— ca cos ot * e ⁼ ~uc, — ue

x    ^y 2    2    ⁷

u - 0

■* 2 V⁶⁵<

—."h względny:

L»^r fa* ^f

[a_tdf + vJ0) = a_xt

* 0 ■

•    t

W) • fvjt)d/+s(0) - a_x ftdt + 0 = a_x -r²

b    1    2

*- ^_ --a.i. 2    2 ^{1 1}

2

a.

2a.

w

3

\

nb

Kinematyka ? 2 6. Kinematyka punktu maicn.ilnepn ^ m«lm /t« */•    2 2 6 Kinematyka punki u muleruilncgn * mchu /in/miyni

233