23 luty 07 (45)

Przyspieszenie dowolnego punktu K wyraża się wzorem

(2.4)

^aK=^aU^+aW = ^a01 + ^aK01 ^{+ a}K01

gdzie:

^a01

przyspieszenie początku układu ruchomego wynikające z jego

translacji (przyspieszenie unoszenia), a_Q1 =

d²r

dt²'

^aK01< ^aK01

odpowiednio przyspieszenie normalne i styczne punktu K względem punktu O, wynikające z rotacji układu ruchomego (przyspieszenie względne).

Przykładem członu wykonującego ruch płaski jest człon 2 (łącznik) mechanizmu korbowo-suwakowego (rys. 2.6).

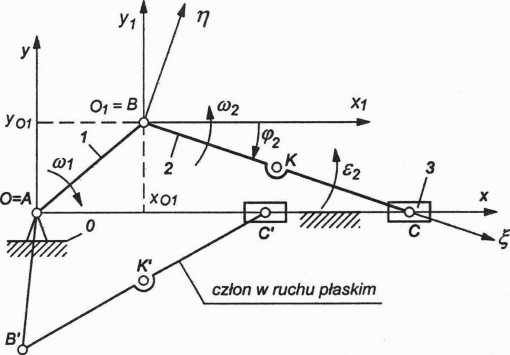
Rys. 2.6. Mechanizm korbowo-suwakowy w układzie współrzędnych

Na rysunkach 2.5 i 2.6 przyjęto jednakowe oznaczenie układów współrzędnych. Na rysunku 2.6 ruchomy układ współrzędnych O^t) związany jest sztywno z łącznikiem 2 mechanizmu korbowo-suwakowego.

Korzystając z przedstawionej wcześniej definicji ruchu płaskiego można wyznaczyć przewodnią prędkości i przyspieszeń łącznika 2 mechanizmu korbowo-suwakowego przedstawionego na rysunku 2.6. Metoda opiera się na składaniu prędkości lub przyspieszeń postępowego ruchu unoszenia i obrotowego ruchu względnego.

Ilustrację graficzną wyznaczania przewodnich prostej ruchomej BKC wykonującej ruch płaski przedstawiono na rysunkach 2.7 i 2.8.

43