23 luty 07 (55)

Oznacza to, że długości rysunkowe wektorów prędkości liniowej oraz przyspieszenia liniowego (normalnego) końca członu napędzającego są równe długości członu napędzającego narysowanego w podziałce k_h (rys. 2.14).

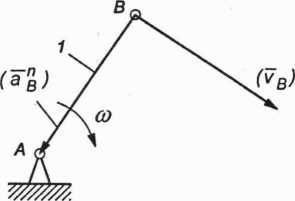
Rys. 2.14. Człon napędzający 1 (korba) z wektorami prędkości i przyspieszeń punktu końcowego

Przyjmowanie takich podziałek nie jest obowiązkowe. W ogólnym przypadku podziałki należy przyjmować w taki sposób, aby wielkość odpowiednich wielo-boków wektorowych zapewniała optymalne wykorzystanie arkusza rysunkowego i zarazem dużą dokładność obliczeń wykreślnych.

Problem dokładności rysowania wielkości wektorowych nie występuje w przypadku wykorzystania do wykreślnego rozwiązywania równań wektorowych programu AutoCAD®. Wówczas odczytane wartości obarczone są tylko błędem wynikającym z obliczeń numerycznych, natomiast wydrukowany w dowolnej podziałce rysunek jest jedynie ilustracją graficzną rozwiązywanych równań. W niniejszej książce wszystkie rysunki zostały wykonane za pomocą programu AutoCAD®.

2.2.3. Grafoanalityczna metoda planów prędkości i przyspieszeń

Metoda planów prędkości i przyspieszeń zwana jest również metodą superpozycji lub metodą wykresów biegunowych. Jest to metoda grafoanalityczna, ponieważ niektóre prędkości i przyspieszenia liniowe oraz prędkości i przyspieszenia kątowe obliczamy z równań algebraicznych, a pozostałe prędkości i przyspieszenia liniowe wyznaczamy, rozwiązując wykreślnie równania wektorowe.

Uzasadnione jest nazywanie metody planów prędkości i przyspieszeń metodą superpozycji, ponieważ prędkości i przyspieszenia charakterystycznych punktów członów mechanizmu są wyznaczane poprzez składanie ruchu unoszenia i ruchu względnego. Natomiast nazwa metoda wykresów biegunowych wynika z techniki rysowania wykresów prędkości i przyspieszeń, które rozpoczynamy rysować od pewnego punktu początkowego zwanego biegunem.

53