23 luty 07 (106)

Znak (-) we wzorze (P2.102) oznacza, że zwrot prędkości kątowej satelity 2 jest przeciwny do zwrotu koła napędzającego 1.

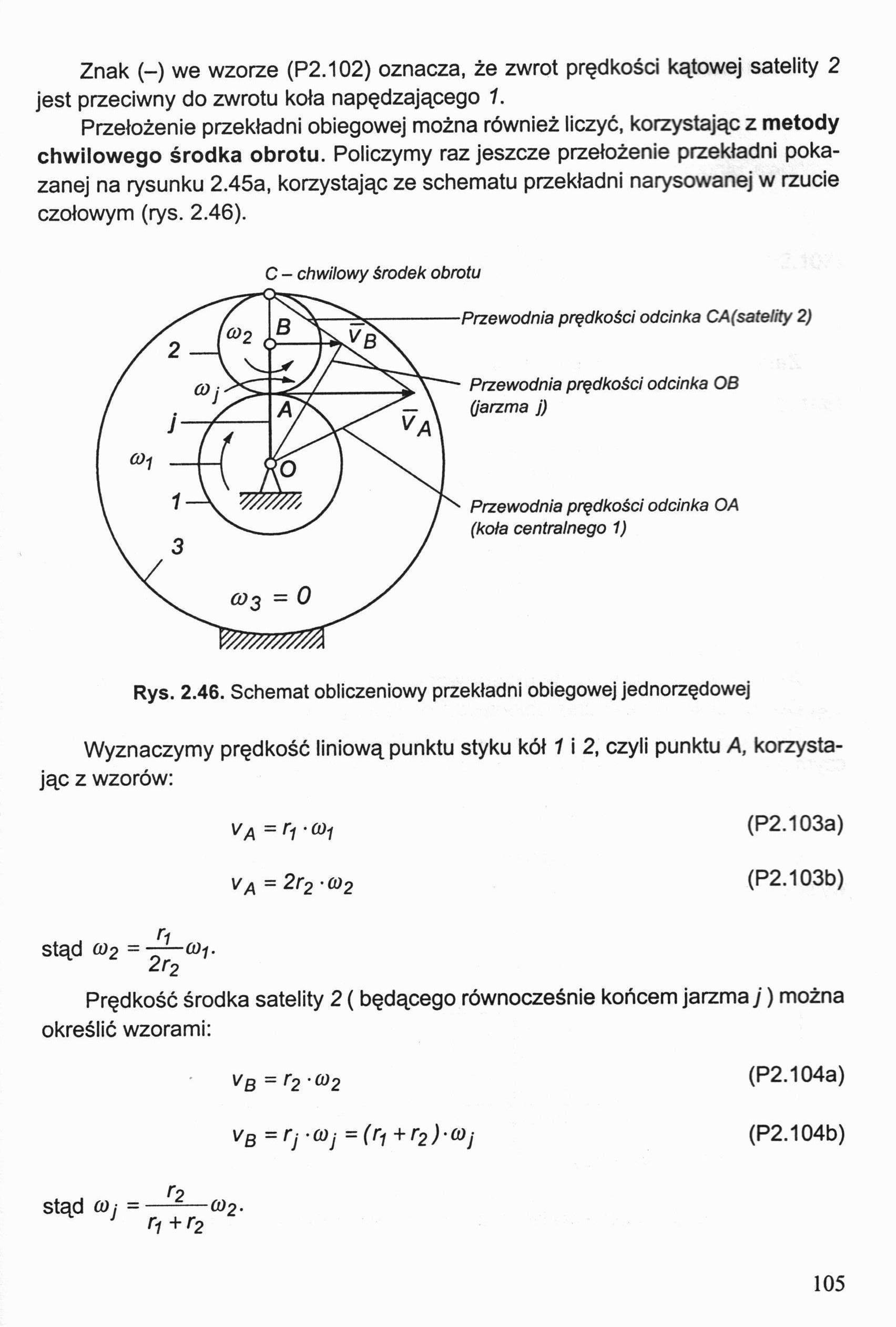
Przełożenie przekładni obiegowej można również liczyć, korzystając z metody chwilowego środka obrotu. Policzymy raz jeszcze przełożenie przekładni pokazanej na rysunku 2.45a, korzystając ze schematu przekładni narysowanej w rzucie czołowym (rys. 2.46).

C - chwilowy środek obrotu

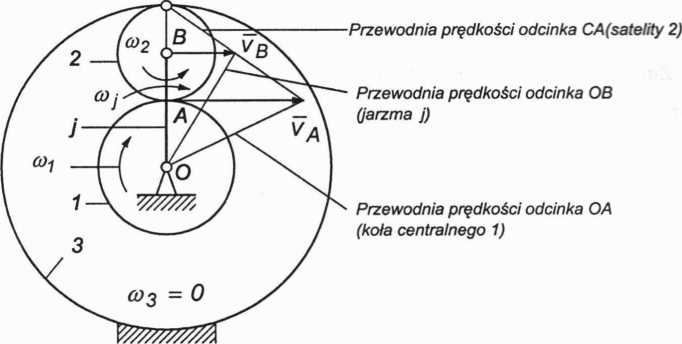
Rys. 2.46. Schemat obliczeniowy przekładni obiegowej jednorzędowej

Wyznaczymy prędkość liniową punktu styku kół 1 i 2, czyli punktu A, korzystając z wzorów:

v_A=r₁-o)i    (P2.103a)

v_A = 2r₂-(02    (P2.103b)

stąd co2 =

2r₂

Prędkość środka satelity 2 ( będącego równocześnie końcem jarzma j) można określić wzorami:

v_B = r₂(o₂    (P2.104a)

v_B = rj -Wj =(r₁ +r₂)-(Oj    (P2.104b)

r?

stąd (Oj =-co₂.

^r1 ^+r2

105