23 luty 07 (101a)

Analiza kinematyczna przekładni obiegowych

Przekładnie obiegowe mają w ogólnym przypadku dwa stopnie swobody (ruchliwość w = 2), jak pokazano na rysunku 2.43a. Jeżeli jednak unieruchomimy względem podstawy jeden z członów, np. koło centralne lub jarzmo, to wówczas przekładnia będzie posiadać jeden stopień swobody: w = 1. Przy tym należy zauważyć, że przekładnia z unieruchomionym jarzmem nie jest już przekładnią obiegową. Przekładnię obiegową o jednym stopniu swobody z unieruchomionym kołem centralnym 3 przedstawia rysunek 2.43b.

Przekładnia obiegowa o dwóch stopniach swobody jest nazywana przekładnią różnicową lub dyferencjałem (rys. 2.43a).

Ta ostatnia nazwa jest szczególnie rozpowszechniona w technice samochodowej i dotyczy przekładni obiegowej z kołami stożkowymi przenoszącej moment napędowy od silnika na koła napędowe.

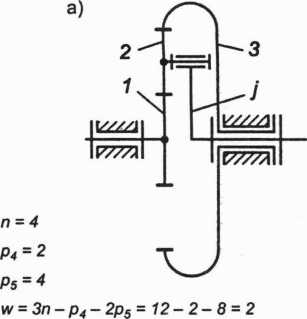
1,3- koła centralne, 2 - satelita, j - jarzmo,

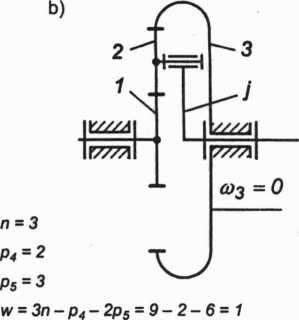
Rys. 2.43. Schematy kinematyczne jednorzędowej przekładni obiegowej: a) przekładnia obiegowa o dwóch stopniach swobody; b) przekładnia obiegowa o jednym stopniu swobody

W celu wyznaczenia przełożenia przekładni obiegowej posłużymy się schematami pokazanymi na rysunku 2.44, gdzie symbolami a i b oznaczone zostały tzw. osiowe elementy przekładni obiegowej, tj. koła centralne, natomiast przez j-oznaczono jarzmo. Na rysunku 2.44a pokazano prędkości kątowe członów ruchomych, tj. co_g, co_b i (Oj przekładni obiegowej, w przypadku kiedy ma ona dwa stopnie swobody, czyli dwa człony (np. a i b ) są członami czynnymi.

Przyjmiemy dalej, że cała przekładnia została wprawiona w ruch z prędkością kątową (-coj). W takim przypadku prędkości kątowe kół centralnych a i b zostaną pomniejszone o wartość coj, natomiast jarzmo stanie się nieruchome coj - coj = 0, (rys. 2.44b), co oznaczamy symbolicznie, wiążąc na rysunku dźwignię jarzma z podstawą.

99