23 luty 07 (103)

Dla przekładni o dwóch stopniach swobody (przekładnia różnicowa, rys. 2.44a), w której dwa człony są członami napędzającymi, np. koła a i b, natomiast jarzmo j jest członem biernym, wyznaczymy wpływ prędkości co_a i w_b na prędkość o)j korzystając ze wzoru Willisa:

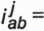
co a ~(Qj

(O_b-(Oj

(2.53)

(2.54)

(o)_b-(Oj)i^Jab = w_a — o)j

COj =

(Oa ~-

‘ab

(Ob

(2.55)

ponieważ zachodzą związki:

1-i

ab

1	u oTó-	i^Jab	1 - i^b- ^1 'aj	1
'i		^1~‘L		ii

_;b

(2.56)

to ostatecznie możemy zapisać

(2.57)

(Oj — ija(Oa "ł"' jb(°b

Praktyczne wykorzystanie wzoru Willisa do obliczania przełożeń przekładni obiegowych pokażemy na przykładach.

Przykład 2.11

Analiza kinematyczna jednorzędowej przekładni obiegowej

Schemat przekładni pokazano na rysunku 2.45.

Dane: co-i, z₇, z₃, co₃ =0, ponieważ koło 3 jest członem nieruchomym.

Obliczyć: przełożenie przekładni /'£• = — oraz (oco₂-

(Oj

Jak zauważymy, nie podano liczby zębów koła 2, gdyż wynika ona z tzw. warunku współosiowości przekładni. Warunek ten określa związek geometryczny pomiędzy średnicami kół zębatych przekładni, które leżąw rozważanym przypadku w jednej płaszczyźnie, mają wspólny moduł, a ponadto dwa z nich mają wspólną oś obrotu.

102