23 luty 07 (13)

Człon swobodny posiada na płaszczyźnie trzy stopnie swobody: dwa przesunięcia x_A, y_A, oraz jeden obrót (p_z, (rys. 1.3). Człon (bryła) wykonuje w tym przypadku ruch płaski, a trzy odebrane stopnie swobody z_A, (p_x, (p_y nazywamy więzami ogólnymi.

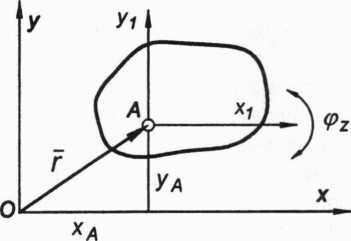
Rys. 1.3. Stopnie swobody członu sztywnego swobodnego na płaszczyźnie

Rozszerzając powyższe rozważania na n członów (brył) swobodnych otrzymamy liczby 6n i 3n oznaczające odpowiednio liczbę stopni swobody przestrzennego i płaskiego swobodnego układu członów.

1.1.3. Para kinematyczna

Para kinematyczna jest to ruchowe połączenie dwóch lub większej liczby członów umożliwiające ich ruch względny.

W połączeniu tym następuje odebranie pewnej liczby stopni swobody (jeden człon ogranicza ruch drugiego) poprzez narzucenie więzów geometrycznych.

Więzy geometryczne są to więzy narzucone przez idealnie sztywne człony, które nie dopuszczają żadnych przemieszczeń względnych na kierunkach odebranych stopni swobody. W mechanice tego typu więzy, które ograniczają tylko swobodę przemieszczania się bryły w przestrzeni, a nie zależą od jej prędkości, nazywamy również więzami holonomicznymi.

Przeciwieństwem więzów geometrycznych (holonomicznych) są więzy kinematyczne (anholonomiczne), zwane więzami podatnymi, które również ograniczają położenie bryły w przestrzeni, lecz zależą od jej prędkości. Tego typu więzy występują przy połączeniach ruchowych członów odkształcalnych.

Zdecydowanie większość połączeń ruchowych członów mechanizmów odbiera możliwość ruchu w obydwu kierunkach, tzn. że człon nie może opuścić powierzchni więzów. Tego typu więzy nazywamy dwustronnymi.

Istnieją jednakże połączenia odbierające możliwość ruchu tylko w jednym kierunku i dopuszczające odrywanie się członów od siebie. Takie więzy nazywamy jednostronnymi. Przykładem może być koło pojazdu posiadające możliwość odrywania się od bieżni.

12