23 luty 07 (131)

Dwa pierwsze równania (3.21) przedstawiają sumy współrzędnych wszystkich sił działających na /'-ty człon względem osi Ox i Oy, a trzecie - sumę współrzędnych momentów wszystkich sił względem dowolnie obranego bieguna.

W metodzie analitycznej można również rozpatrywać równowagę grup strukturalnych, nie jest to jednak konieczne. Metodę analityczną analizy kinetostatycznej mechanizmu przedstawimy na przykładzie czworoboku przegubowego.

Przykład 3.1

Należy wyznaczyć reakcje w parach kinematycznych mechanizmu czworoboku oraz moment równoważący przyłożony do członu napędzającego 1 dla zadanego układu sił zewnętrznych jak na rysunku 3.15. Przeprowadzić analizę z pominięciem sił ciężkości i bezwładności (analizę statyczną).

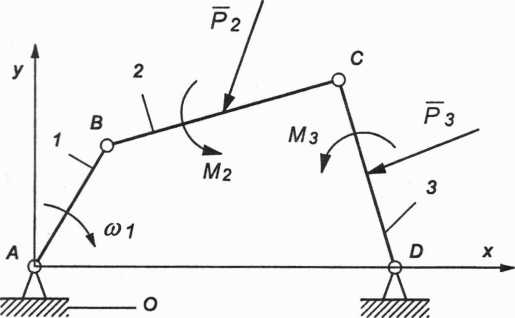
Rys. 3.15. Czworobok przegubowy z zadanym układem sił zewnętrznych Rozwiązanie

Sprawdzamy warunek (3.19) statycznej wyznaczalności mechanizmu: 3-3 = = 24 + 1=9. Warunek jest spełniony. Zadanie może zostać rozwiązane analitycznie. Wymaga napisania dziewięciu warunków równowagi.

Uwalniamy od więzów poszczególne człony mechanizmu (rys. 3.16), a następnie piszemy warunki równowagi:

X ^Pi( 1 )x ⁼0-    X ^Pi< l)y ~0<    X ^iA( 1) ⁼ G

lPi(2_)x=0, ;Z^pi(2,y=0, ZM_iB(2) = 0    (P3.1)

lPi(3)x=0, lP_i(3)y=0, lM_iC(3₎=0

130